Эллиптические уравнения
Решение эллиптических уравнений в частных производных реализовано только для единственного типа задач – двумерного уравнения Пуассона.
Это уравнение содержит вторые производные функции u(х,у) по двум пространственным переменным:
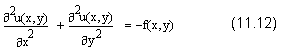
Уравнение Пуассона описывает, например, распределение электростатического поля u(х,у) в двумерной области с плотностью заряда f (x,y), или (см. разд. 11.1.2) стационарное распределение температуры u(х,у) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью f (х,у).
Примечание
Несмотря на то, что применение встроенных функций, описанных в данном разделе, анонсировано разработчиками Mathcad только для уравнения Пуассона, их можно применять и для решения других уравнений, даже необязательно эллиптического типа. О том, как осуществить такие расчеты, написано в конце данного раздела.
Уравнение Пуассона с нулевыми граничными условиями
Корректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В Mathcad решение ищется на плоской квадратной области, состоящей из (M+1)х(M+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант – это нулевые граничные условия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию multigrid:
- multigrid (F,ncycie) – матрица решения уравнения Пуассона размера (м+1)х(м+1) на квадратной области с нулевыми граничными условиями:
- F – матрица размера (M+1)х(M+1), задающая правую часть уравнения Пуассона;
- ncycle – параметр численного алгоритма (количество циклов в пределах каждой итерации).
Внимание!
Сторона квадрата расчетной области должна включать точно N=2n шагов, т. е. 2n+1 узлов, где n – целое число.
Параметр численного метода ncycle в большинстве случаев достаточно взять равным 2. Листинг 11.7 содержит пример использования функции multigrid для расчета краевой задачи на области 33х33 точки и точечным источником тепла в месте, задаваемом координатами (15.20) внутри этой области.
Листинг 11.7. Решение уравнения Пуассона с нулевыми граничными условиями:
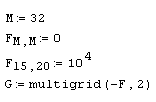
В первой строке листинга задается значение м=32, в двух следующих строках создается матрица правой части уравнения Пуассона, состоящая из всех нулевых элементов, за исключением одного, задающего расположение источника. В последней строке матрице с присваивается результат действия функции multigrid. Обратите внимание, первый ее аргумент сопровождается знаком "минус", что соответствует записи правой части уравнения Пуассона (11.11). Графики решения показаны на рис. 11.17 и 11.18 в виде трехмерной поверхности и линий уровня соответственно.
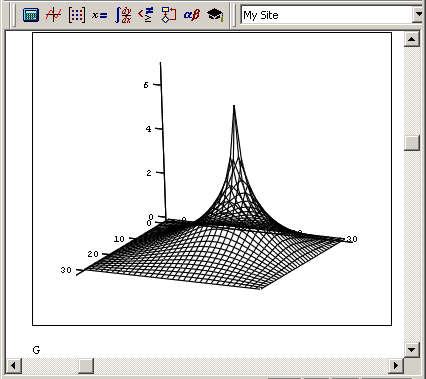
Рис. 11.17. График поверхности решения уравнения Пуассона (продолжение листинга 11.7)
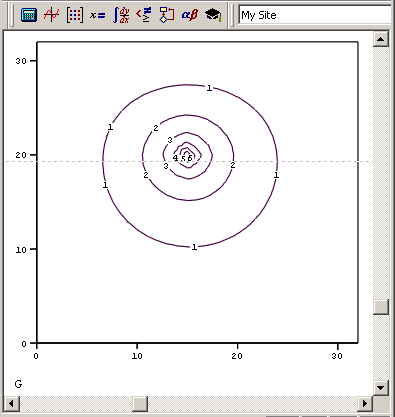
Рис. 11.18. График линий уровня решения уравнения Пуассона (продолжение листинга 11.7)