Эллиптические уравнения
Разностная схема для решения уравнения Пуассона
Несмотря на отсутствие сведений в справочной системе Mathcad о решении других линейных дифференциальных уравнений в частных производных, кроме уравнения Пуассона, сделать это возможно с помощью той же функции relax (см. предыдущий разд.). Для этого нужно правильным образом задать коэффициенты разностной схемы.
Начнем с пояснения выбора этих коэффициентов (см. листинг 11.8) для уравнения Пуассона. Согласно основным идеям метода сеток (см. разд. 11.2), для дискретизации обеих пространственных производных в уравнении (11.12) следует использовать по три соседних узла вдоль каждой из координат. Поэтому уравнение Пуассона (11.12) может быть записано в разностной форме при помощи шаблона типа "крест" (рис. 11.20). В этом случае, после приведения подобных слагаемых в разностных уравнениях коэффициенты разностной схемы будут такими, как показано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для явной и неявных схем решения уравнения теплопроводности см. на рис. 11.6 и 11.11 соответственно).
Теперь, если вы сравните полученные числа с константами, которые присвоены элементам матриц-аргументов функции relax (см. листинг 11.8), то увидите, что они как раз и описывают вычисленные нами только что коэффициенты разностной схемы "крест". Таким образом, нетрудно сообразить, что с помощью встроенной функции relax можно решать и другие линейные дифференциальные уравнения в частных производных, которые можно аппроксимировать схемой типа "крест" или схемой, являющейся ее составной частью. Конечно, для того чтобы использовать эту встроенную функцию для другого уравнения, необходимо будет составить соответствующую разностную схему.
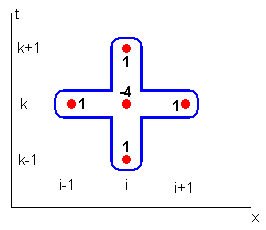
Рис. 11.20. Шаблон аппроксимации уравнения Пуассона "крест"
Решение уравнения диффузии тепла при помощи функции relax
Приведем пример применения встроенной функции relax для решения другого уравнения в частных производных (т. е. не уравнения Пуассона, для которого она изначально предназначена). Вычислим при помощи этой функции решение уже хорошо нам знакомого однородного линейного уравнения теплопроводности (см. разд. 11.1.2). Будем использовать явную разностную схему, шаблон которой изображен на рис. 11.6. Для того чтобы "приспособить" для явной схемы функцию relax, требуется только задать ее аргументы в соответствии с коэффициентами, показанными на шаблоне (см. рис. 11.6). Программа, реализующая таким способом явную схему, представлена на листинге 11.9. Число Куранта в этом листинге обозначено переменной с, как и положено явной разностной схеме, она выдает устойчивое решение только для C<1.
Листинг 11.9. Решение уравнения теплопроводности при помощи функции relax:
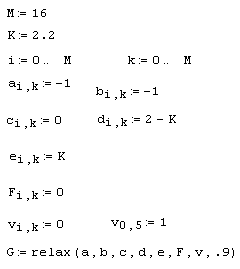
Результат действия программы листинга 11.9 показан на рис. 11.21 в виде трехмерной поверхности. Если сравнить рис. 11.21 с рис. 11.4, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 11.4 нетрудно узнать сечения этой поверхности плоскостями t=const. Еще раз подчеркнем, что использовать встроенную функцию можно только для тех уравнений, которые допускают построение разностной схемы типа "крест" (см. рис. 11.17) или составного фрагмента этой схемы.
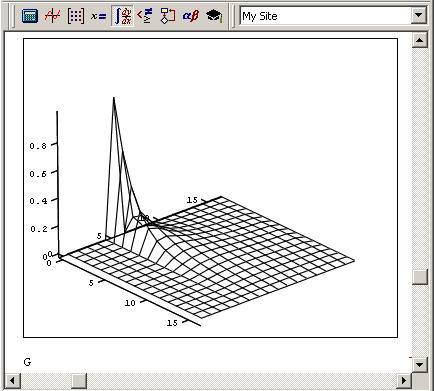
Рис. 11.21. Решение уравнения теплопроводности с помощью функции relax (продолжение листинга 11.9)