Пример: нормальное (Гауссово) распределение
Приведем несколько примеров, позволяющих почувствовать математический смысл рассмотренных функций на примере случайной величины х, распределенной по нормальному закону с µ =0 и σ =1 (листинги 12.1-12.5).
Листинг 12.1. Вероятность того, что х будет меньше 1.881:
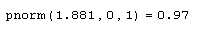
Листинг 12.2. 97-% квантиль нормального распределения:
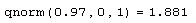
Листинг 12.3. Вероятность того, что х будет больше 2:
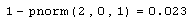
Листинг 12.4. Вероятность того, что х будет находиться в интервале (2.3):
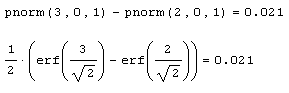
Листинг 12.5. Вероятность того, что |x|<2:

Обратите внимание, что задачи двух последних листингов решаются двумя разными способами. Второй из них связан с еще одной встроенной функцией erf, называемой функцией ошибок (или интегралом вероятности, или функцией Крампа).
- erf(x) – функция ошибок.
- erfc(x)=1-erf(x).
Математический смысл функции ошибок ясен из листинга 12.5. Интеграл вероятности имеет всего один аргумент, в отличие от функции нормального распределения. Исторически последняя пересчитывалась через табулированный интеграл вероятности по формулам, приведенным в листинге 12.6 для произвольных значений параметров µ и σ (листинг 12.6).
Листинг 12.6. Вероятность того, что х будет в интервале (2.3):
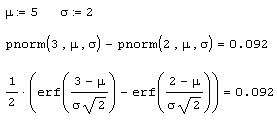
Если вы имеете дело с моделированием методами Монте-Карло, то в качестве генератора случайных чисел с нормальным законом распределения применяйте встроенную функцию rnorm. В листинге 12.7 ее действие показано на примере создания двух векторов по M=500 элементов в каждом с независимыми псевдослучайными числами x1i и х2i распределенными согласно нормальному закону. О характере распределения случайных элементов векторов можно судить по рис. 12.5. В дальнейшем мы будем часто сталкиваться с генерацией случайных чисел и расчетом их различных средних характеристик.
Листинг 12.7. Генерация двух векторов с нормальным законом распределения:
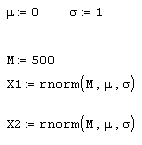
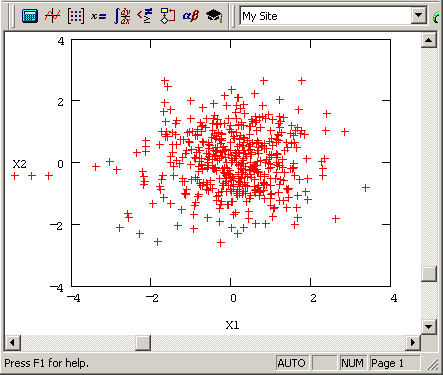
Рис. 12.5. Псевдослучайные числа с нормальным законом распределения (продолжение листинга 12.7)
