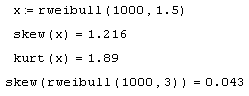Новые функции корреляционного анализа сигналов. Коэффициенты асимметрии и эксцесса.
В Mathcad 12 появились две функции, связанные с корреляционной обработкой сигналов и изображений:
- correl (x,y) – вектор, представляющий значения коэффициента ковариации двух векторов;
- correl 2d(A, K) – матрица, равная ковариации матрицы-аргумента и матрицы-окна:
- х,у – векторы;
- А – матрица-прототип;
- K – матрица-окно (размера, меньшего чем А).
Смысл действия одномерной функции correl заключается в последовательном сдвиге одного вектора относительно другого, перемножении и суммировании их элементов, стоящих в таком положении друг напротив друга. Это не совсем ковариация в терминах математической статистики, поскольку не осуществляется нормировки (деления полученной суммы на число перемноженных элементов).
Работа двумерной функции correl 2d состоит в последовательном позиционировании "маленькой" матрицы (окна) на фоне "крупной" (прототипа), перемножении их элементов, находящихся друг над другом, и суммировании их. В результате получается элемент матрицы корреляции, соответствующий центрам наложения матрицы-прототипа и матрицы-окна. Обе эти функции играют определенную роль в задачах обработки сигналов.
Коэффициенты асимметрии и эксцесса
Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящей через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например, нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.
Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной – коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.
Для расчета коэффициентов асимметрии и эксцесса в Mathcad имеются две встроенные функции:
- kurt (х) – коэффициент эксцесса (kurtosis) выборки случайных данных х;
- skew(x) – коэффициент асимметрии (skewness) выборки случайных данных X.
Примеры расчета коэффициентов асимметрии и эксцесса для распределения Вейбулла приведены в листинге 12.17.
Листинг 12.17. Расчет выборочных коэффициентов асимметрии и эксцесса: