Примеры: Выборочная оценка дисперсии и среднего нормальной случайной величины
Для проверки гипотезы (листинг 12.14) рассчитывается (а/2)-квантиль распределения Стьюдента т, который служит критическим значением для принятия или отклонения гипотезы. Если соответствующее выборочное значение T по модулю меньше т, то гипотеза принимается (считается верной). В противном случае гипотезу следует отвергнуть.
Листинг 12.14. Проверка гипотезы о математическом ожидании при неизвестной дисперсии:
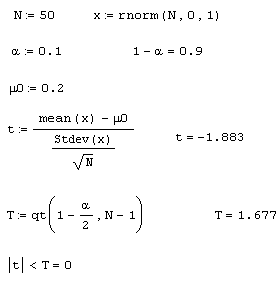
В последней строке листинга вычисляется истинность или ложность условия, выражающего решение задачи. Поскольку условие оказалось ложным (равным не 1, а 0), то гипотезу необходимо отвергнуть.
На рис. 12.8 показано распределение Стьюдента с N-1 степенью свободы, вместе с критическими значениями, определяющими соответствующий интервал. Если t (оно тоже показано на графике) попадает в него, то гипотеза принимается; если не попадает (как произошло в данном случае) – отвергается. Если увеличить а, ужесточив критерий, то границы интервала будут сужаться по сравнению с показанными на рисунке.
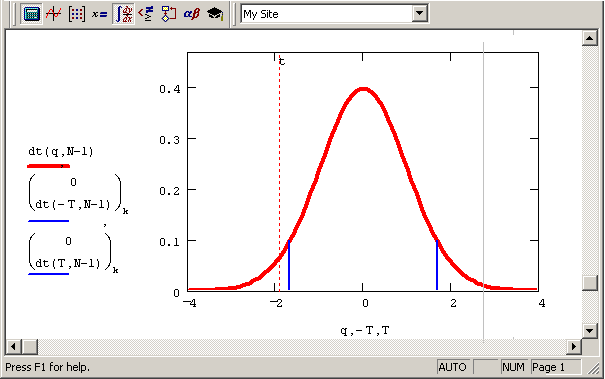
Рис. 12.8. К задаче проверки статистических гипотез (продолжение листинга 12.14)
В листинге 12.15 приводится альтернативный способ проверки той же самой гипотезы, связанный с вычислением значения не квантиля, а самого распределения Стьюдента.
Листинг 12.15. Другой вариант проверки гипотезы (продолжение листинга 12.14):
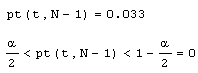
Мы разобрали только два характерных примера статистических вычислений. Однако с помощью Mathcad легко решаются самые разнообразные задачи математической статистики.
Примечание
Большое количество задач разобрано в Ресурсах в рубрике Statistics (Статистика) Быстрых шпаргалок.
