Пример: нормальное (Гауссово) распределение
В теории вероятности доказано, что сумма различных независимых случайных слагаемых (независимо от их закона распределения) оказывается случайной величиной, распределенной согласно нормальному закону (так называемая центральная предельная теорема). Поэтому нормальное распределение хорошо моделирует самый широкий круг явлений, для которых известно, что на них влияют несколько независимых случайных факторов.
Перечислим еще раз встроенные функции, имеющиеся в Mathcad для описания нормального распределения вероятностей:
- dnorm(x,µ, σ) – плотность вероятности нормального распределения;
- pnorm(х,µ,σ) – функция нормального распределения;
- сnorm(х) – функция нормального распределения для µ=0, σ=1;
- qnorm(P,µ,σ) – обратная функция нормального распределения;
- rnorm(M,µ, σ) – вектор м независимых случайных чисел, каждое из которых имеет нормальное распределение:
- х – значение случайной величины;
- P – значение вероятности;
- µ – математическое ожидание;
- σ – среднеквадратичное отклонение.
Математическое ожидание и дисперсия являются, по сути, параметрами распределения. Плотность распределения для трех пар значений параметров показана на рис. 12.3. Напомним, что плотность распределения dnorm задает вероятность попадания случайной величины х в малый интервал от х до х+Δх. Таким образом, например, для первого графика (сплошная линия) вероятность того, что случайная величина х примет значение в окрестности нуля, приблизительно в три раза больше, чем вероятность того, что она примет значение в окрестности х=2. А значения случайной величины большие 5 и меньшие -5 и вовсе очень маловероятны.
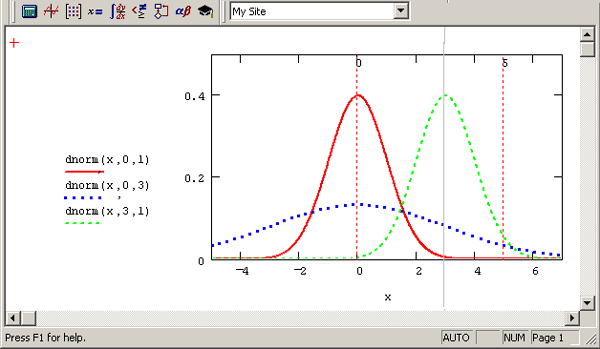
Рис. 12.3. Плотность вероятности нормальных распределений
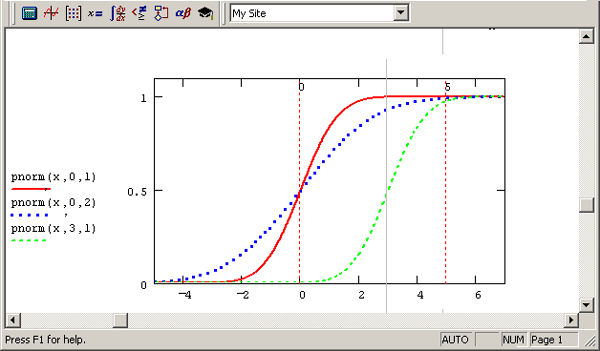
Рис. 12.4. Нормальные функции распределения
Функция распределения F(x) (cumulative probability) – это вероятность того, что случайная величина примет значение, меньшее или равное х. Как следует из математического смысла, она является интегралом от плотности вероятности в пределах от -∞ до х. Функции распределения для упомянутых нормальных законов изображены на рис. 12.4. Функция, обратная F(x) (inverse cumulative probability), называемая еще квантилем распределения, позволяет по заданному аргументу р определить значение х, причем случайная величина будет меньше или равна х с вероятностью р.
Примечание
Здесь и далее графики различных статистических функций, показанные на рисунках, получены с помощью Mathcad без каких-либо дополнительных выражений в рабочей области.
