Эллиптические уравнения
Уравнение Пуассона с произвольными граничными условиями
В более сложных случаях, например, для решения краевой задачи с ненулевыми условиями на границах, следует использовать другую встроенную функцию relax, имеющуюся в Mathcad:
- relax(a,b,c,d,e,F,v,rjac) – матрица решения дифференциального уравнения в частных производных на квадратной области, полученного с помощью алгоритма релаксации для метода сеток:
- a,b,c,d,e – квадратные матрицы коэффициентов разностной схемы, аппроксимирующей дифференциальное уравнение;
- F – квадратная матрица, задающая правую часть дифференциального уравнения;
- v – квадратная матрица граничных условий и начального приближения к решению;
- rjac – параметр численного алгоритма (спектральный радиус итераций Якоби);
Параметр численного алгоритма характеризует скорость сходимости итераций. Он должен быть числом от о до 1. В матрице граничных условий v необходимо задать только граничные элементы, исходя из значения краевых условий по периметру расчетной области. Прочие (внутренние) элементы этой матрицы служат для задания начального приближения к решению.
Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомой функции в каждой точке. Если начальное приближение выбрано удачно, то можно надеяться, что алгоритм сойдется ("релаксирует") к правильному решению.
Внимание!
Все матрицы, задающие как коэффициенты разностной схемы а, b, с, d, e, граничные условия v, так и само решение F, должны иметь одинаковый размер (M+1)х(M+1), соответствующий размеру расчетной области. При этом целое число м обязательно должно быть степенью двойки: м=2n.
Решение уравнения Пуассона с тремя источниками разной интенсивности при помощи функции relax приведено в листинге 11.8.
Листинг 11.8. Решение уравнения Пуассона с помощью функции relax:
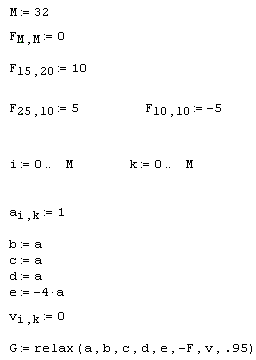
Первые три строки имеют тот же смысл, что и в предыдущем листинге. Только вместо одного источника тепла взято их другое распределение – один сильный источник, один более слабый и один сток тепла. В следующих шести строках задаются коэффициенты разностной схемы. Отложим их обсуждение до последнего раздела этой главы, ограничившись утверждением, что для решения уравнения Пуассона коэффициенты должны быть взяты именно такими, как показано в листинге 11.8. В предпоследней строке задана матрица нулевых граничных условий и нулевых начальных приближений, а в последней матрице с присваивается результат действия функции relax. График полученного решения в виде линий уровня показан на рис. 11.19.
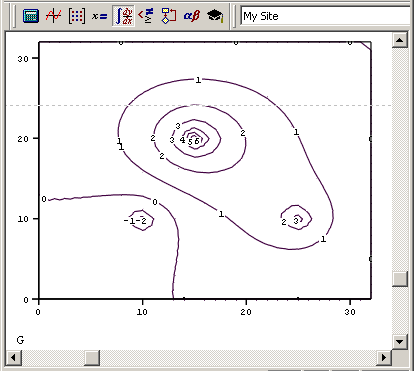
Рис. 11.19. Решение уравнения Пуассона с помощью функции relax (продолжение листинга 11.8)
