Разностные схемы
Рассмотрим одномерное уравнение теплопроводности (11.3) и на его примере разберем наиболее часто использующийся для численного решения уравнений в частных производных метод сеток.
Выпишем еще раз само уравнение:
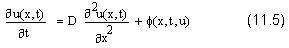
Выпишем также и начальные:
u(x,0) = u0(x), (11.6)
И граничные условия которые необходимы для правильной с математической точки зрения постановки задачи:
u(0, t) = f0(t), u(L, t) = f1(t), (11.7)
Основная идея численного решения уравнений в частных производных очень похожа на метод решения краевых задач для ОДУ, рассмотренный нами в предыдущей главе. Основным отличием от ОДУ является необходимость дискретизации уравнения не по одной, а по нескольким переменным (в зависимости от размерности задачи).
Таким образом, сначала следует покрыть расчетную область (x,t) сеткой и использовать затем узлы этой сетки для разностной аппроксимации уравнения. В результате, вместо поиска непрерывных зависимостей u(x,t) достаточно будет отыскать значения функции в узлах сетки (а ее поведение в промежутках между узлами может быть получено при помощи построения какой-либо интерполяции). По этой причине дискретное представление функции и часто называют сеточной функцией.
Поскольку уравнения в частных производных по определению зависят от производных неизвестных функций по нескольким переменным, то способов дискретизации этих уравнений может быть, как правило, несколько. Конфигурацию узлов, используемую для разностной записи уравнений в частных производных на сетке, называй шаблоном, а полученную систему разностных уравнений – разностной схемой.
О принципах построения разностных схем и, в частности, о классах явных и неявных схем мы уже подробно говорили на примере краевых задач для ОДУ (см. разд. 10.4.1), поэтому, излишне не повторяясь, перейдем к рассмотрению типичных особенностей уравнений в частных производных, которые возникают при разработке и реализации разностных схем.
