Встроенные функции для решения уравнений в частных производных. Параболические и гиперболические уравнения.
Как видно из предыдущего раздела, с уравнениями в частных производных вполне можно справиться и не прибегая к специфическим средствам Mathcad. Между тем в версиях Mathcad 11 (и выше) имеется несколько встроенных функций, при помощи которых можно автоматизировать процесс решения дифференциальных уравнений в частных производных. Рассмотрим в данном разделе основные аспекты их применения, отмечая не только инструкции по их применению, описанные разработчиками Mathcad, но также и некоторые "скрытые" возможности этих функций.
Разработчики впервые применили дополнительные встроенные функции для решения параболических и гиперболических уравнений в частных производных в версии Mathcad 11, отлично осознавая значимость этих задач для современного исследователя и инженера. Предусмотрены два варианта решения: при помощи вычислительного блока Given/pdesolve, а также при помощи встроенной функции numol. Первый путь проще в применении и нагляднее, зато второй позволяет автоматизировать процесс решения уравнений в частных производных, например, если нужно включить его в качестве составного шага в более сложную Mathcad-программу.
Вычислительный блок Given/pdesolve
Встроенная функция pdesolve применяется в рамках вычислительного блока, начинающегося ключевым словом Given, и пригодна для решения различных гиперболических и параболических уравнений. Она предназначена для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока Given), зависящего от времени t и пространственной координаты х, имеет целый набор различных аргументов и работает следующим образом:
- pdesolve(u,x,xrange,t,trange,[xpts],[tpts])) – Возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x,t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме:
- u – явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр;
- х – пространственная координата (имя аргумента неизвестной функции);
- xrange – пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
- t – время (имя аргумента неизвестной функции);
- trange – расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
- xpts – количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
- tpts – количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).
В качестве примера использования функции pdesolve (листинг 11.4) используем то же самое одномерное уравнение теплопроводности (11.5) с граничными и начальными условиями (11.6) и (11.7).
Листинг 11.4. Решение одномерного уравнения теплопроводности:
Для корректного использования функции pdesolve предварительно, после ключевого слова Given, следует записать само уравнение и граничные условия при помощи логических операторов (для их ввода в Mathcad существует специальная панель). Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x,t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции pdesolve). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например, uxx(,t), для обозначения второй производной функции и по пространственной координате х.
Как видно из рис. 11.14, на котором изображены результаты расчетов по листингу 11.4, встроенная функция с успехом справляется с уравнением диффузии, отыскивая уже хорошо знакомое нам решение. Заметим, что использование встроенной функции pdesolve связано с довольно громоздкими вычислениями, которые могут отнимать существенное время.
Примечание
Как вы можете заметить, выбирать величину шага по пространственной и временной переменным может как сам алгоритм, так и пользователь (неявным образом, через число узлов сетки). Читателю предлагается повторить вычисления листинга 11.4 для различных комбинаций параметров (главным образом, числа узлов сетки), чтобы проверить, в каких случаях алгоритм встроенной функции справляется с задачей, выдавая верное решение, а в каких дает сбой.
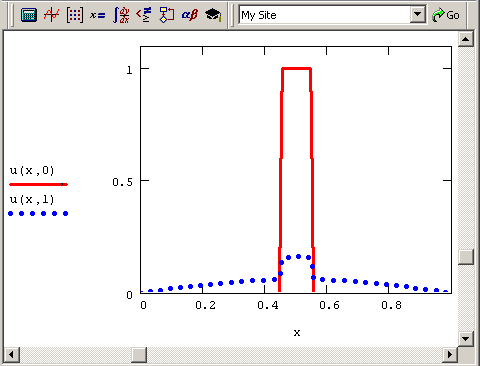
Рис. 11.14. Решение уравнения диффузии тепла при помощи встроенной функции pdesoive (листинг 11.4)