Встроенные функции для решения уравнений в частных производных. Параболические и гиперболические уравнения.
Встроенная функция numol
Альтернативный вариант решения дифференциальных уравнений в частных производных заключается в применении еще одной встроенной функции numol, которая реализует тот же самый алгоритм сеток, позволяя вручную задать большинство его параметров:
- numol(xrange,xpts,trange,tpts,Npde,Nae,rhs,init,bc) – Возвращает матрицу решения дифференциального уравнения в частных производных, представляющую искомую сеточную функцию в каждой точке по пространственной (по строкам) и временной координате (по столбцам). Если решается не одно уравнение, а система уравнений, то результатом является составная матрица, образованная путем слияния (слева-направо) матриц со значениями каждой искомой сеточной функции:
- Npde – общее количество дифференциальных уравнений в частных производных в системе;
- Nae – общее количество дополнительных алгебраических уравнений, которые также могут входить в систему;
- rhs – векторная функция, определяющая систему дифференциальных и алгебраических уравнений (формат этого и двух следующих матричных параметров объяснен в листинге 11.9);
- init – векторная функция, определяющая начальные условия для каждой неизвестной функции;
- be – функциональная матрица граничных условий;
- xrange – пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
- xpts – количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
- trange – расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
- tpts – количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно);
Пример решения волнового уравнения при помощи функции numol приведен в листинге 11.6, особое внимание в котором мы призываем уделить формату представления векторов rhs, init и be, а также принципу извлечения отдельных сеточных решений из матрицы-результата. График решения, показанный на рис. 11.16, полезно сравнить с результатом применения вычислительного блока из предыдущего раздела (см. листинг 11.5 и рис. 11.15).
Листинг 11.6. Решение волнового уравнения при помощи функции numol:

Как вы видите, функция numol имеет еще большее число аргументов, нежели pdesolve, и позволяет автоматизировать применение метода сеток. Однако пользоваться ею намного сложнее, чем вычислительным блоком, поскольку и уравнения, и начальные и граничные условия должны быть записаны в специальном формате. Применение функции numol оправданно, когда необходимо включить решение уравнений в частных производных в более сложные вычисления в качестве подпрограммы, организовать серию расчетов с меняющимся параметром, подготовить анимацию графиков решения и т. п.
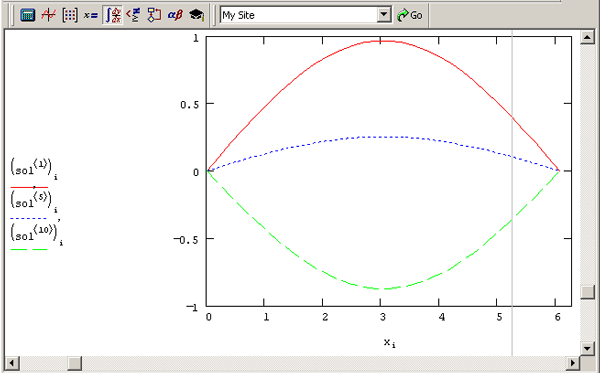
Рис. 11.16. Решение волнового уравнения (продолжение листинга 11.6)
Именно в целях визуализации решения параболических и гиперболических уравнений в частных производных использование функции numol наиболее полезно. График решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее и воспринимается несравненно лучше, если он оформлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу FRAME и затем применить команду View › Animate (Вид › Анимация) (см. разд. 13.3.2).
