О возможности решения многомерных уравнений
Все, что было сказано до сих пор, касалось исключительно способов решения одномерных (в смысле пространственных координат) уравнений. И алгоритмы разностных схем, и встроенные функции, включая появившиеся в 11-й версии (см. следующий разд.), относились к уравнениям, зависящим от одной пространственной координаты.
Можно ли при помощи Mathcad решать двумерные или трехмерные (пространственные) уравнения? С точки зрения программирования пользователем численных алгоритмов типа метода сеток принципиальных ограничений нет. Разумеется, если сначала аккуратно выписать разностную схему соответствующего многомерного дифференциального уравнения, то вполне возможно запрограммировать ее при помощи описанных нами средств. Самым главным противодействием будет существенное увеличение времени расчетов. Простая оценка необходимого количества операций показывает, что если ввод зависимости уравнения от второй пространственной координаты многократно увеличивает число разностных уравнений, которые должны решаться при реализации каждого шага по времени.
К примеру, если используется пространственная сетка из 100 узлов по каждой координате, то вместо 102 разностных уравнений на каждом шаге придется решать уже 104 уравнений, т. е. объем вычислений сразу же возрастает в 100 раз. Вообще говоря, пакет Mathcad не является экономичной средой вычислений, и бороться с их сильно возрастающим объемом следует пользователю еще на этапе разработки алгоритма. Хорошим примером такой борьбы может служить применение специфических алгоритмов, типа метода прогонки (см. разд. "Алгоритм прогонки"этой главы).
Приведем некоторые дополнительные замечания, связанные с возможностью осуществить редукцию громоздких (в смысле организации вычислений) двумерных задач к более простым. Рассмотрим ради примера двумерное уравнение теплопроводности (11.1) без источника с нулевыми граничными условиями и некоторым начальным двумерным распределением температуры по расчетной поверхности:
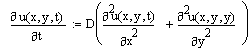
Произведем дискретизацию данного уравнения по временной координате, заменяя первую производную ее разностным аналогом и несколько перегруппировывая слагаемые и множители:
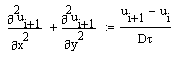
Как вы видите, мы используем неявную разностную схему, заранее заботясь о том, чтобы разностная задача была более устойчивой. Здесь ui(x,y) – известная с предыдущего шага по времени функция двух пространственных переменных, а u1+1(х,у) – функция, подлежащая определению при реализации каждого шага по времени.
Посмотрим на полученную задачу с несколько другой стороны – а именно как на дифференциальное уравнение относительно неизвестной функции двух переменных ui+ 1(x,y). Подчеркнем, что такое уравнение получается для каждого шага по времени, т. е. для реализации всей разностной схемы требуется решить большое число таких уравнений.
С предложенной точки зрения, на каждом временном шаге необходимо решить некоторое двумерное эллиптическое линейное уравнение, причем его граничные условия определяются граничными условиями исходной задачи. Это уравнение очень похоже на уравнение Пуассона с той лишь разницей, что в его правую часть, описывающую источник, входит неизвестная функция (к счастью, линейно). Таким образом, зависимость от найденного на предыдущем шаге по времени решения определяется зависимостью от него источника, т. е. правой части.
Суммируя сказанное, можно констатировать, что если вы имеете запрограммированный алгоритм решения выписанного эллиптического уравнения, чуть более сложного, чем уравнение Пуассона, то его с легкостью можно использовать в качестве подпрограммы реализации разностной схемы двумерного уравнения теплопроводности. Забегая вперед, приходится отметить, что, к сожалению, встроенные функции Mathcad для решения уравнения Пуассона в данном случае не годятся в качестве такой подпрограммы, поскольку предполагают независимость источника от самой неизвестной функции, и могут справляться лишь с правой частью, зависящей только от пространственных координат (см. разд. 11.3.2).
Не будем далее останавливаться на способах решения многомерных уравнений, ограничившись этими замечаниями относительно путей оптимизации алгоритмов их решения.