Явная схема Эйлера
Линейное уравнение
Сделанные замечания относительно реализации явной схемы для уравнения диффузии тепла сразу определяют алгоритм ее программирования в Mathcad. Для решения задачи нужно аккуратно ввести в листинг соответствующие формулы при помощи элементов программирования.
Решение системы разностных уравнений (11.9) для модели без источников тепла, т.е. ф(x,T,t)=0 и постоянного коэффициента диффузии D=const приведено в листинге 11.1. В его первых трех строках заданы шаги по временной и пространственной переменным t и А, а также коэффициент диффузии о, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия соответственно. Затем приводится возможное программное решение разностной схемы, причем функция пользователя v(t) задает вектор распределения искомой температуры в каждый момент времени (иными словами, на каждом слое), задаваемый целым числом t.
Листинг 11.1. Явная схема для линейного уравнения теплопроводности:
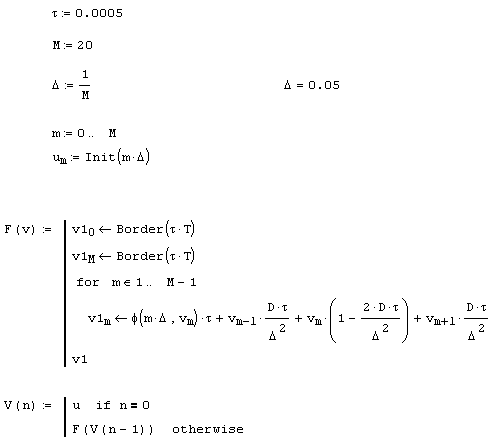
Начальное распределение температуры вдоль расчетной области и решение для двух моментов времени показано на рис. 11.7 сплошной, пунктирной и штриховой линиями соответственно. Физически такое поведение вполне естественно – с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается.
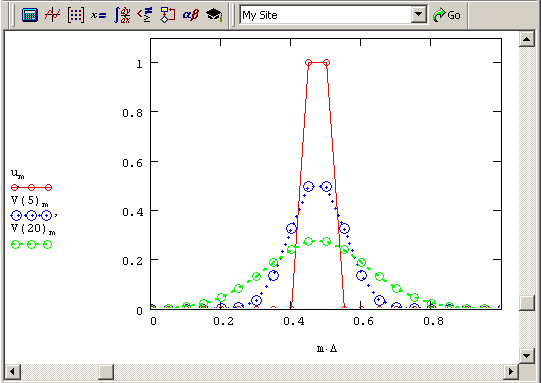
Рис. 11.7. Решение линейного уравнения теплопроводности (продолжение листинга 11.1)
Примечание
Несколько забегая вперед, заметим, что показанное на рис. 11.7 решение и соответствует коэффициенту Куранта С=0.4. Попробуйте осуществить расчет с увеличенным временным шагом, чтобы коэффициент с был больше 1, и посмотрите, что из этого получится (такой расчет и его объяснение приведены ниже в разд. "Устойчивость").
