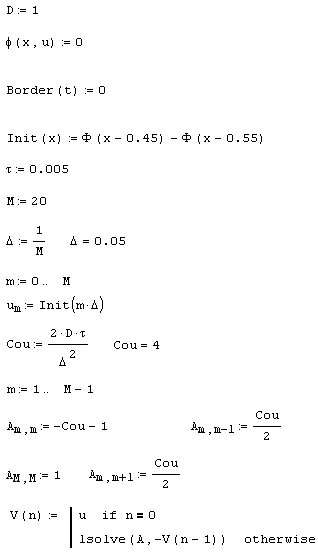Неявная схема Эйлера
В отличие от явной схемы Эйлера, неявная является безусловно-устойчивой (т. е. не выдающей "разболтки" ни при каких значениях коэффициента Куранта). Однако ценой устойчивости является необходимость решения на каждом шаге по времени системы алгебраических уравнений.
Построение неявной разностной схемы
Чтобы построить неявную разностную схему для уравнения диффузии, используем шаблон, изображенный на рис. 11.11, т. е. для дискретизации пространственной производной будем брать значения сеточной функции с верхнего (неизвестного) слоя по времени. Таким образом, разностное уравнение для (i,k)-го узла будет отличаться от уравнения для явной схемы (11.8) только индексами по временной координате в правой части:
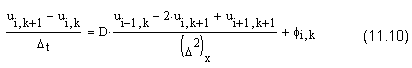
Если привести подобные слагаемые, то получится система уравнений, связывающая для каждого 1-го узла три неизвестных значения сеточной функции (в самом этом узле и в соседних с ним слева и справа узлах). Множители при неизвестных значениях сеточной функции в узах шаблона показаны на рис. 11.11 в виде подписей, подобно тому, как это было сделано для явной схемы (см. рис. 11.6).
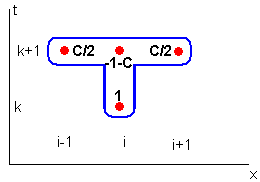
Рис. 11.11. Шаблон неявной схемы для уравнения теплопроводности
Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а ф в его правой части может зависеть только от первой степени и. Поэтому система уравнений (11.10) для всех пространственных узлов 1=1…м-l является линейной системой, что существенно упрощает ее решение (поскольку известно, что для линейных систем с ненулевым определителем решение существует и является единственным). Напомним, что для получения замкнутой системы линейных уравнений необходимо дополнить данный набор разностных уравнений граничными условиями, т. е. известными значениями сеточной функции для i=0 и i=M.
Примечание
Если рассматривать нелинейный случай, то на каждом шаге по времени пришлось бы решать систему нелинейных уравнений, число решений которых могло бы быть большим, и среди них требовалось бы отыскать нужное, а не паразитное решение.
Для реализации неявной схемы, таким образом, можно использовать комбинацию средств программирования Mathcad и встроенной функции решения системы линейных уравнений isolve. Один из возможных способов решения предложен в листинге 11.2. Большая часть этого листинга является вводом параметров задачи (шагов, начальных и граничных условий), и только в последней его строке определяется функция пользователя, вычисляющая сеточную функцию на каждом временном слое (при помощи встроенной функции решения системы линейных уравнений isolve). В нескольких предыдущих строках листинга (после расчета коэффициента Куранта сои) формируется матрица системы уравнений А, которая записывается в подходящем для Mathcad виде, как это сделано в листинге 11.2. Как несложно убедиться, столбец правых частей разностных уравнений выражается вычисленными значениями сеточной функции с предыдущего слоя.
Результаты расчетов по неявной схеме показаны на рис. 11.12 и, как видно, они дают примерно те же результаты, что и в случае применения явной схемы (см. рис. 11.7). Обратите внимание, что решение устойчиво при любых значениях коэффициента Куранта (в том числе и больших 1), поскольку, как следует из соответствующих положений теории численных методов, неявная схема является безусловно-устойчивой.
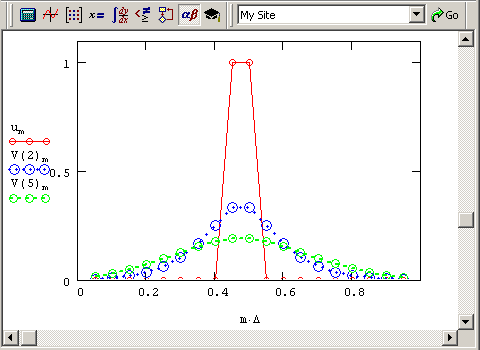
Рис. 11.12. Решение линейного уравнения теплопроводности при помощи неявной схемы на первом слое по времени (листинг 11.2)
Листинг 11.2. Неявная схема для линейного уравнения теплопроводности:
