Методы Монте-Карло. Генерация псевдослучайных чисел.
Для моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло, обязанные своим названием европейскому центру азартных игр, основанных на случайных событиях. Основная идея этих методов состоит в создании определенной последовательности случайных чисел, моделирующей тот или иной эффект, например, шум в физическом эксперименте, случайную динамику биржевых индексов и т. п. Фактически все содержание предыдущего раздела (см. разд. 12.2) являлось примером реализации методов Монте-Карло, поскольку содержало расчет тех или иных статистических характеристик имитационных данных, полученных при помощи генератора случайных чисел.
Рассмотрим еще несколько типовых задач, относящихся к методам Монте-Карло, попутно изучая соответствующие возможности, заложенные в Mathcad.
Генерация псевдослучайных чисел
Как уже отмечалось (см. разд. 12.1.1), для генерации M – компонентного вектора независимых псевдослучайных чисел имеется ряд встроенных функций, реализующих различные типы статистических распределений и имеющих вид r*(M,раr), где * – идентификатор, а par – список параметров конкретного распределения. В частности, генератор нормальных псевдослучайных чисел был рассмотрен ранее (см. разд. 12.1.2), а для равномерного распределения предусмотрено две встроенных функции:
- runif(M,а,b) – вектор м независимых случайных чисел, каждое из которых имеет равномерное распределение;
- rn d(x) – случайное число, имеющее равномерную плотность распределения на интервале (0,х):
- х – значение случайной величины;
- Р – значение вероятности;
- (а, b) – интервал, на котором случайная величина распределена равномерно.
Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad – дань традиции, применяемой в большинстве сред программирования. Возможно, именно скалярный тип этой функции определяет простоту и привычность ее использования в расчетах моделей типа Монте-Карло.
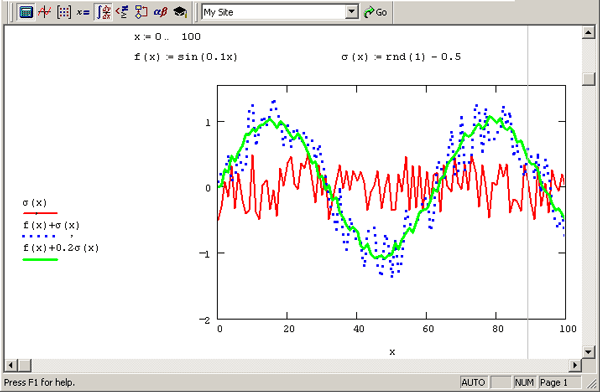
Рис. 12.9. Модель сигнал/шум с равномерным законом распределения
Рисунок 12.9 демонстрирует широко распространенный прием моделирования, основанный на смеси некоторого полезного сигнала f(х) и шумовой компоненты а, что характерно для типичного физического эксперимента. В качестве шума используется серия равномерно распределенных псевдослучайных чисел. Различные соотношения интенсивностей сигнала и шума определяют различные условия модельной задачи и позволяют эффективно протестировать алгоритмы, которые разработаны для ее решения.
Примечание
Более сложные статистические расчеты для модели сигнал/шум приведены в листинге 12.24 (см. разд. 12.3.4).
Параметры генераторов псевдослучайных чисел
В Mathcad применяются типичные алгоритмы генерации последовательностей псевдослучайных чисел, которые используют в качестве "отправной точки" некоторое начальное (или отправное) значение (seed value). Это начальное значение используется для того, чтобы совершить над ним определенные математические действия (к примеру, взять остаток от деления на некоторое другое число) и получить в итоге первое псевдослучайное число последовательности. Затем те же математические операции совершаются с первым числом для получения второго, и т. д.
Несложно догадаться, что если использовать все время одно и то же начальное значение генератора псевдослучайных чисел, то, открывая всякий раз новый документ со встроенной функцией получения тех или иных псевдослучайных чисел, будет выдаваться в точности одна и та же их последовательность. Сами числа внутри последовательности будут "почти" случайными (значимость этого "почти" будет зависеть только от качества алгоритма генерации), но вот сама последовательность при каждом открытии документа будет одной и той же.
Примечание
Вы можете сами убедиться в идентичности выдаваемых последовательностей псевдослучайных чисел, открывая и закрывая несколько раз документ с рис. 12.9 или любой документ с иным датчиком случайных чисел, описанных в данном разделе. Любопытным также будет эксперимент по последовательному применению нескольких встроенных функций генерации псевдослучайных чисел в пределах одного документа.
Для того чтобы иметь возможность поменять саму последовательность сгенерированных случайным датчиком чисел, в Mathcad 11 (и выше) предусмотрена новая возможность явного определения используемого им начального значения. Для этого вызовите командой меню Tools › Worksheet Options (Сервис › Опции документа) диалог Worksheet Options (Опции документа) и на вкладке Built-in Variables (Встроенные переменные) введите желаемое (целое) число в поле ввода Seed value for random Bombers (Начальное значение для генератора псевдослучайных чисел).
Альтернативный способ заключается в использовании соответствующей встроенной функции непосредственно в документе:
- seed(x) – функция установки нового начального значения для генератора псевдослучайных чисел:
- х – новое начальное значение для генератора псевдослучайных чисел (целое число от 1 до 2147483647).