Интерполяция и регрессия
Посвятим данную главу самым простым методам обработки данных – интерполяции-экстраполяции и регрессии. Будем считать, что основным объектом исследования будет выборка экспериментальных данных, которые, чаще всего, представляются в виде массива, состоящего из пар чисел (xi,yi) (проблеме ввода/вывода числовых данных во внешние файлы посвящен заключительный раздел этой главы). В связи с этим возникает задача аппроксимации дискретной зависимости y(xi) непрерывной функцией f(x). Функция f (х), в зависимости от специфики задачи, может отвечать различным требованиям:
- f(x) должна проходить через точки (xi,yi), т.е .f (xi)=yi, i=1..n. В этом случае (см. разд. 13. Г) говорят об интерполяции данных функцией f (х) во внутренних точках между xi или экстраполяции за пределами интервала, содержащего все хi;
- f (х) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(xi), не обязательно проходя через точки (xi,yi). Такова постановка задачи регрессии (см. разд. 13.2), которую во многих случаях также можно назвать сглаживанием данных. Вообще говоря, сглаживание является частным случаем фильтрации данных (см. главу 14), основанной на уменьшении шумовой компоненты измерений.
Различные виды построения аппроксимирующей зависимости f (х) иллюстрирует рис. 13.1. На нем исходные данные обозначены кружками, интерполяция отрезками прямых линий – пунктиром, линейная регрессия – наклонной прямой линией, а фильтрация – жирной гладкой кривой. Эти зависимости приведены в качестве примера и отражают лишь малую часть возможностей Mathcad по обработке данных. Вообще говоря, в Mathcad имеется целый арсенал встроенных функций, позволяющий осуществлять самую различную регрессию, интерполяцию и экстраполяцию.
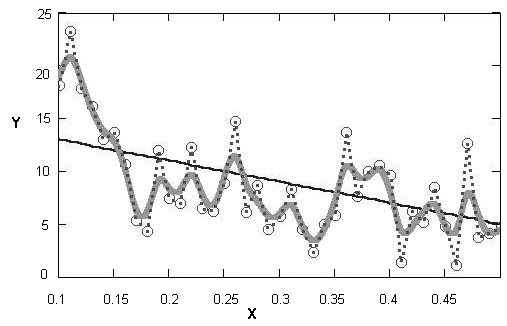
Рис. 13.1. Разные задачи аппроксимации данных
