Иллюстрированный самоучитель по MathCAD 12

Регрессия. Линейная регрессия.

Задачи математической регрессии имеют смысл приближения выборки данных (xi,yi) некоторой функцией f(x), определенным образом минимизирующей совокупность ошибок |f(xi)-yi|. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f (х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.

Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных (x_i,y_i).

Самый простой и наиболее часто используемый вид регрессии – линейная. Приближение данных (x_i,y_i) осуществляется линейной функцией у(х) = b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 13.14). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и b вычисляются из условия минимизации суммы квадратов ошибок | b+ax_i-y_i |.

Примечание 1
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (x_i, y_i) другими зависимостями у(х). Исключение рассмотрено в листинге 13.9.

Примечание 2
Различным расчетным аспектам реализации метода наименьших квадратов, в большинстве случаев сводящимся к решению систем алгебраических линейных уравнений, была посвящена значительная часть главы 8.

Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 13.7 и 13.8. Результат обоих листингов получается одинаковым (рис. 13.14):

• line (х, у) – вектор из двух элементов (b,а) коэффициентов линейной регрессии b+ах;
• intercept (х, у) – коэффициент ь линейной регрессии;
• slope (x,y) – коэффициент а линейной регрессии:
  • х – вектор действительных данных аргумента;
  • у – вектор действительных данных значений того же размера.

Листинг 13.7. Линейная регрессия:

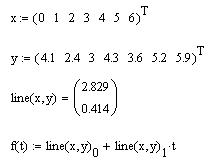
Листинг 13.8. Другая форма записи линейной регрессии:

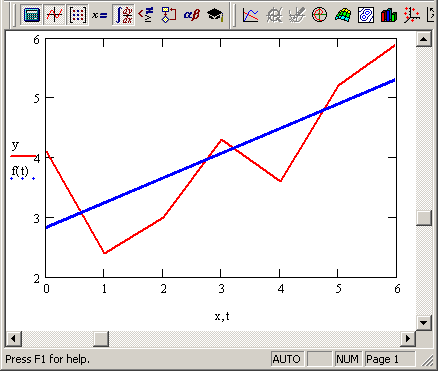
Рис. 13.14. Линейная регрессия (продолжение листинга 13.7 или 13.8)

В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов а и b (листинг 13.9):

• medfit(x,y) – вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной регрессии b-ах:
  • х, у – векторы действительных данных одинакового размера.

Листинг 13.9. Построение линейной регрессии двумя разными методами (продолжение листинга 13.7):

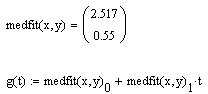
Различие результатов среднеквадратичной и медиан-медианной регрессии иллюстрируется на рис. 13.15.

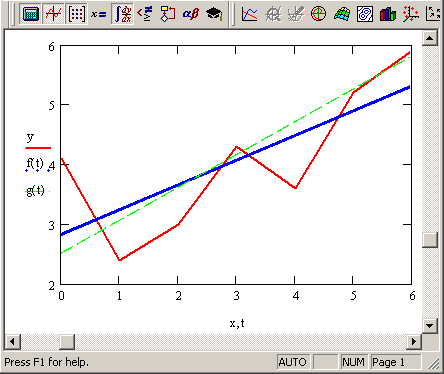
Рис. 13.15. Линейная регрессия по методу наименьших квадратов и методу медиан (продолжение листингов 13.7 и 13.9)