Полиномиальная регрессия
Двумерная полиномиальная регрессия
По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 13.1.5), Mathcad позволяет приблизить множество точек Zi,j(xi,yj) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.
- regress (x,z,k) – вектор коэффициентов для построения полиномиальной регрессии данных.
- loess (x,z,span) – вектор коэффициентов для построения регрессии данных отрезками полиномов.
- interp(s,x,z,v) – скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами:
- s – вектор вторых производных, созданный одной из сопутствующих функций loess или regress.
- х – матрица размерности Nx2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у).
- z – вектор действительных данных размерности N.
- span – параметр, определяющий размер отрезков полиномов.
- k – степень полинома регрессии (целое положительное число).
- v – вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
Внимание!
Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, которая требует их представления в виде матрицы NxN). В связи с этим данные представляются как вектор.
Двумерная полиномиальная регрессия иллюстрируется листингом 13.12 и рис. 13.18. Сравните стиль представления данных для двумерной регрессии с представлением тех же данных для двумерной сплайн-интерполяции (см. листинг 13.6) и ее результаты с исходными данными (см. рис. 13.12) и их сплайн-интерполяцией (см. рис. 13.13).
Листинг 13.12. Двумерная полиномиальная регрессия:
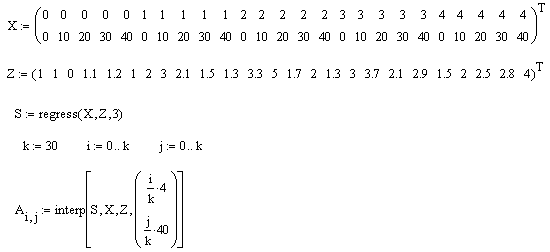
Примечание
Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например, z, в качестве вектора, а не строки).
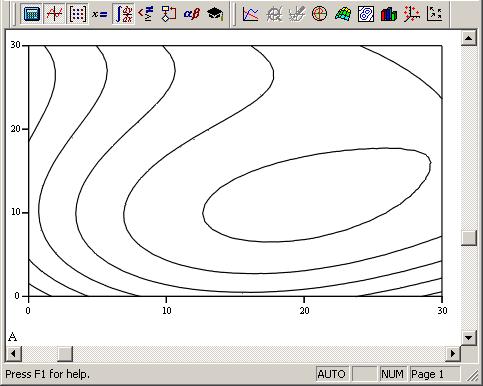
Рис. 13.18. Двумерная полиномиальная регрессия (продолжение листинга 13.12)
