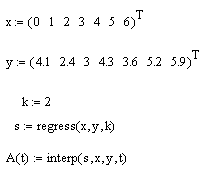Иллюстрированный самоучитель по MathCAD 12

Полиномиальная регрессия

В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.

Полиномиальная регрессия означает приближение данных (x_i,y_i) полиномом k-й степени: A(x)=a+bx+cx² +dx³ +…+hx^k (рис. 13.16). При k=i полином является прямой линией, при k=2 – параболой, при k=3 – кубической параболой и т. д. Как правило, на практике применяются k<5.

Примечание
Для построения регрессии полиномом k-й степени необходимо наличие, по крайней мере, (k+1) точек данных.

В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции (см. разд. 13.1.2):

• regress (х, у, k) – вектор коэффициентов для построения полиномиальной регрессии данных;
• interp(s,x,y, t) – результат полиномиальной регрессии:
  • s=regress(х,у,k);
  • x – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
  • у – вектор действительных данных значений того же размера;
  • k – степень полинома регрессии (целое положительное число);
  • t – значение аргумента полинома регрессии;

Внимание!
Для построения полиномиальной регрессии после функции regress вы обязаны использовать функцию interp.

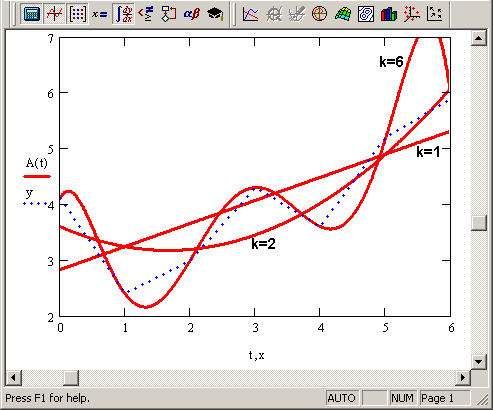
Рис. 13.16. Регрессия полиномами разной степени (коллаж результатов листинга 13.10 для разных k)

Пример полиномиальной регрессии квадратичной параболой приведен в листинге 13.10.

Листинг 13.10. Полиномиальная регрессия: