Иллюстрированный самоучитель по MathCAD 12

Интерполяция. Линейная интерполяция.

Для построения интерполяции-экстраполяции в Mathcad имеется несколько встроенных функций, позволяющих "соединить" точки выборки данных (x_i,y_i) кривой разной степени гладкости. По определению интерполяция означает построение функции А(Х), аппроксимирующей зависимость у(х) в промежуточных точках (между x_i). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках x_i значения интерполяционной функции должны совпадать с исходными данными, т. е. A(x_i)=y (x_i).

Примечание
Везде в этом разделе, при рассказе о различных типах интерполяции будем использовать вместо обозначения А(х) другое имя ее аргумента A(t), чтобы не путать вектор данных х и скалярную переменную t.

Линейная интерполяция

Самый простой вид интерполяции – линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(х) состоит из отрезков прямых, соединяющих точки (рис. 13.2).

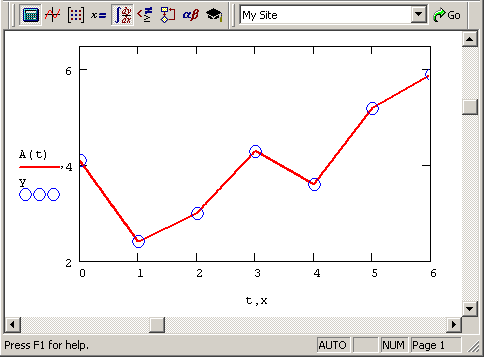
Рис. 13.2. Линейная интерполяция (продолжение листинга 13.1)

Для построения линейной интерполяции служит встроенная функция linterp (листинг 13.1):

• linterp (х,у,t) – функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью:
  • х – вектор действительных данных аргумента;
  • у – вектор действительных данных значений того же размера;
  • t – значение аргумента, при котором вычисляется интерполирующая функция.

Внимание!
Элементы вектора х должны быть определены в порядке возрастания, т. е. X_l<X₂<X₃<…<X_N.

Листинг 13.1. Линейная интерполяция:

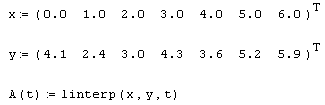
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:

1. Ввести векторы данных х и у (первые две строки листинга).
2. Определить функцию linterp (х, у, t).
3. Вычислить значения этой функции в требуемых точках, например, linterp(х,у,2.4)=3.52, или linterp(х,у,6)=5.9, или постройте ее График, как показано на рис. 13.2.

Примечание
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция A(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале (0.6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 13.3) Mathcad по умолчанию соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).

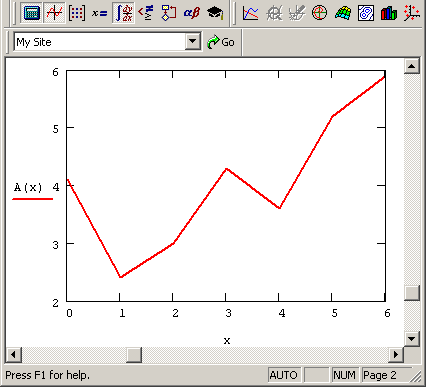
Рис. 13.3. Обычное построение графика функции от векторной переменной х (продолжение листинга 13.1)