Сплайн-экстраполяция
Все описанные в предыдущих разделах типы интерполяции работают также и как функции экстраполяции данных. Для вычисления экстраполяции достаточно просто указать соответствующее значение аргумента, которое лежит за границами рассматриваемого интервала. С этой точки зрения разницы в применении в Mathcad между интерполяцией и экстраполяцией нет.
На практике при построении экстраполяции следует соблюдать известную осторожность, не забывая о том, что ее успех определяется значимостью ближайших к границе интервала точек. Чем дальше от них вы будете пытаться экстраполировать зависимость, заданную экспериментальными точками, тем сомнительнее будет результат.
Сказанное иллюстрируется рис. 13.8 и 13.9, на которых изображена линейная (пунктир на обоих графиках) и сплайн – (сплошные кривые) экстраполяция. На рис. 13.8 используется линейная сплайн-экстраполяция при помощи функции ispline (см. рис. 13.5 в качестве примера интерполяции), а на рис. 13.9 – функции кубического сплайна cspline (что соответствует листингу 13.2 и рис. 13.4). Видно, что вдали от рассматриваемого интервала результаты экстраполяции совершенно различны, что, конечно, объясняется тем, что она является ни чем иным как параболической зависимостью.
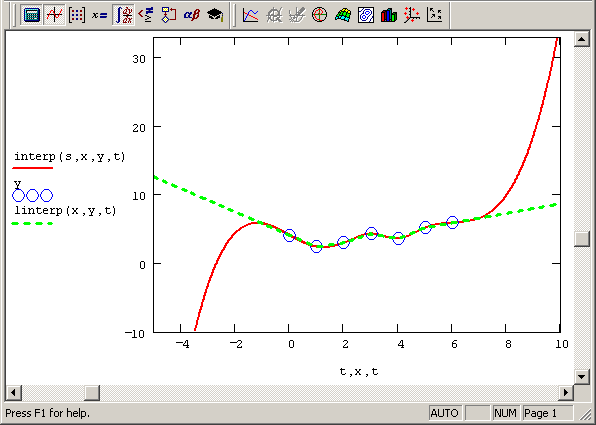
Рис. 13.8. Линейная сплайн-экстраполяция
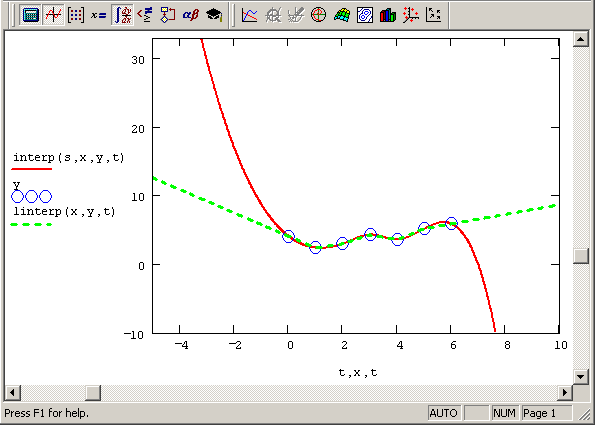
Рис. 13.9. Квадратичная сплайн-экстраполяция (продолжение листинга 13.2)
