Полиномиальная регрессия
Регрессия отрезками полиномов
Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress (листинг 13.11 и рис. 13.17):
- loess (х, у, span) – вектор коэффициентов для построения регрессии данных отрезками полиномов;
- interp(s,x,y,t) – результат полиномиальной регрессии:
- s=loess(х,у,span);
- х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у – вектор действительных данных значений того же размера;
- span – параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).
Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).
Листинг 13.11. Регрессия отрезками полиномов:
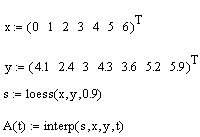
Совет
Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.
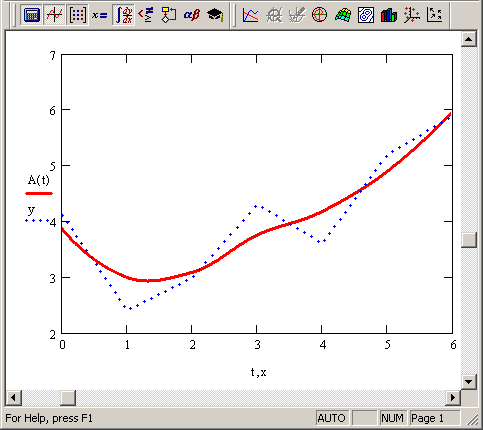
Рис. 13.17. Регрессия отрезками полиномов (продолжение листинга 13.11)
