Другие типы регрессии
Кроме рассмотренных, в Mathcad встроено еще несколько видов трехпараметрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а, b, с. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а, b, с.
- expfit (х, у, g) – регрессия экспонентой f (х) =aebx +c.
- igsfit (x,y,g) – регрессия логистической функцией f (x)=a/ (1+bе-сх).
- sinfit (x,y,g) – регрессия синусоидой f (x) =a-sin (х+b) +с.
- pwfit(x,y,g) – регрессия степенной функцией f (х)=а-хb+с.
- logfit (х, у, g) – регрессия логарифмической функцией f (x)=aln(x+b) +c.
- infit (x,y) – регрессия двухпараметрической логарифмической функцией f (x)=aln(x)+b:
- х – вектор действительных данных аргумента.
- у – вектор действительных значений того же размера.
- g – вектор из трех элементов, задающий начальные значения а, b, с.
Примечание
Правильность выбора начальных значений можно оценить по результату регрессии – если функция, выданная Mathcad, хорошо приближает зависимость у (х), значит, они были подобраны удачно.
Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 13.13 и на рис. 13.19. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а, b, с, а в последней строке через эти коэффициенты определена искомая функция f (х).
Листинг 13.13. Экспоненциальная регрессия:
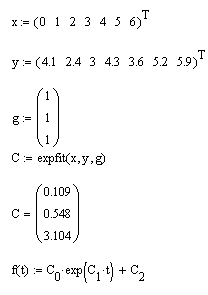
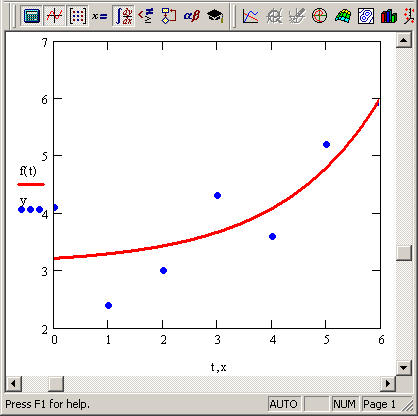
Рис. 13.19. Экспоненциальная регрессия (продолжение листинга 13.13)
Примечание
Многие задачи регрессии данных различными двухпараметрическими зависимостями у(х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.
