Пример: огибающая и фаза нормального случайного процесса
Завершим разговор о моделировании случайных процессов примером, часто встречающимся в задачах статистической радиофизики. Рассмотрим модель, представляющую собой сумму гармонической функции и нормально распределенной шумовой компоненты, которая хорошо описывает передачу сигнала в электронных устройствах в условиях помех (листинги 12.24-12.25) и называется узкополосным нормальным процессом. Как известно, узкополосный процесс представим в виде E(t)exp(iф(t)), где случайные функции E(t) и ф(t) называются, соответственно, его огибающей и фазой. Мы приведем пример нулевого сигнала (т. е. расчет огибающей и фазы чистого случайного процесса), хотя минимальное изменение листинга 12.25 даст вам возможность промоделировать и ненулевые значения сигнала.
Первая половина листинга 12.24 представляет собой подготовительный этап, заключающийся в генерации двух векторов с нормальным распределением вероятности. Из курса математической статистики известно, что узкополосный гауссов процесс можно представить в виде, приведенном в последней строке листинга 12.24, причем случайные функции A(t) и C(t) называются квадратурными составляющими нормального случайного процесса. Графики A(t) и C(t) показаны на рис. 12.13. Листинг 12.25 содержит суммирование полученных шумовых компонент с составляющими гармонического сигнала и выдает в качестве результата функции E(t) и ф(t) (они показаны на рис. 12.14).
Листинг 12.14. Квадратурные составляющие нормального случайного процесса:

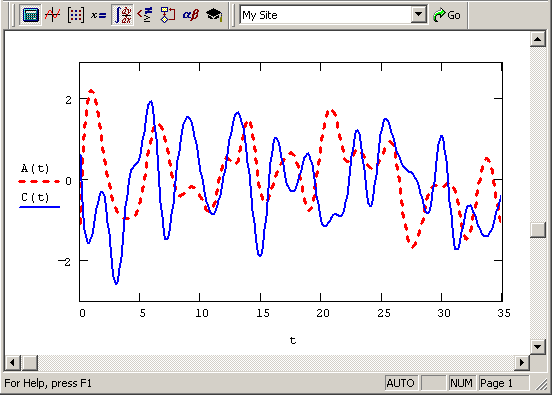
Рис. 12.13. Квадратурные составляющие случайного процесса (продолжение листинга 12.24)
Листинг 12.25. Огибающая и фаза нормального случайного процесса (продолжение листинга 12.24):
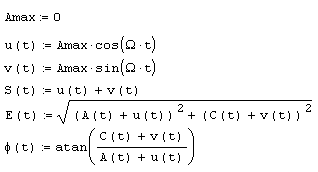
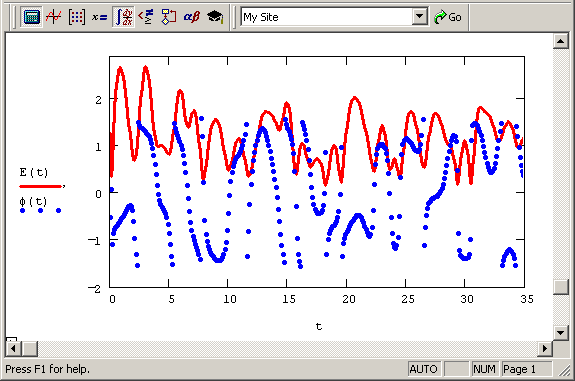
Рис. 12.14. Огибающая и фаза нормального случайного процесса (продолжение листингов 12.24-12.25)
