Примеры: Выборочная оценка дисперсии и среднего нормальной случайной величины
Типовые задачи математической статистики связаны с получением тех или иных интервальных и точечных оценок различных параметров случайной выборки. Приведем пример двух задач, иллюстрирующих назначение и принципы применения введенных в предыдущих разделах статистических функций.
Интервальная оценка дисперсии
Требуется определить числовой интервал (L, U), внутри которого будет лежать с вероятностью 1-а=75% дисперсия нормальной случайной величины, исходя из объема выборки в N чисел. Эта задача решается в статистике с помощью χ2 -распределения (листинг 12.13).
Листинг 12.13. Интервальное оценивание дисперсии:
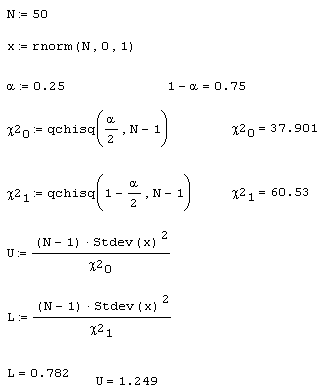
Указанный интервал называется (1-a) доверительным интервалом. Обратите внимание на использование при решении данной задачи функции stdev (с прописной буквы) для расчета выборочного стандартного отклонения. В статистике часто встречаются выражения, которые более удобно записывать через функции в такой нормировке, именно для этого они и появились в Mathcad.
Проверка статистических гипотез
В статистике рассматривается огромное число задач, связанных с проверкой тех или иных гипотез н. Разберем пример простой гипотезы. Пусть имеется выборка N чисел с нормальным законом распределения и неизвестными дисперсией и математическим ожиданием. Требуется принять или отвергнуть гипотезу H о том, что математическое ожидание закона распределения равно некоторому числу µ0 = 0. 2.
Задачи проверки гипотез требуют задания уровня критерия проверки гипотезы а, который описывает вероятность ошибочного отклонения истинной н. Если взять ее очень малым, то гипотеза, даже если она ложная, будет почти всегда приниматься; если, напротив, взять а близкими 1, то критерий будет очень строгим, и гипотеза, даже верная, скорее всего, будет отклонена.
В нашем случае гипотеза состоит в том, что µ0 = 00.2, а альтернатива– что µ0#0. 2. Оценка математического ожидания, как следует из курса классической статистики, решается с помощью распределения Стьюдента с параметром N-1 (этот параметр называется степенью свободы распределения).
