Жесткие краевые задачи
Один из случаев, когда применение разностных схем может быть очень полезным, связан с решением жестких краевых задач (подробнее о жестких ОДУ читайте в главе 11). В частности, рассматриваемая задача о встречных световых пучках становится жесткой при увеличении коэффициента ослабления а(х) в несколько десятков раз. Например, при попытке решить ее с а(х): = 100 с помощью листинга 10.2 вместо ответа выдается сообщение об ошибке "Can't converge to a solution. Encountered too many integration steps" (Не сходится к решению. Слишком много шагов интегрирования). Это и неудивительно, поскольку жесткие системы характерны тем, что требуют исключительно малого значения шага в стандартных алгоритмах.
Для жестких задач неприменимы и явные разностные схемы, о которых рассказывалось в предыдущем разделе (см. разд. 10.3.1). Результат расчетов по программе листинга 10.6, например с а(х): = 20 (рис. 10.9), дает характерную для неустойчивых разностных схем "разболтку" – колебания нарастающей амплитуды, не имеющие ничего общего с реальным решением.
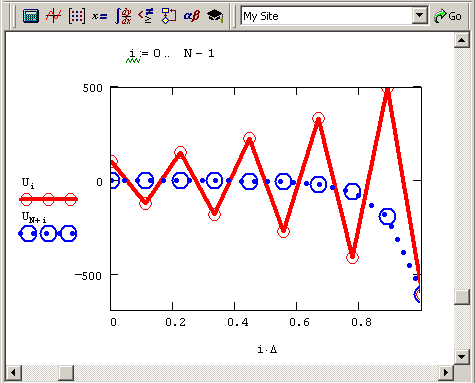
Рис. 10.9. Неверное решение жесткой краевой задачи по неустойчивой явной разностной схеме
Выходом из положения будет использование неявных разностных схем. Применительно к нашей задаче достаточно заменить правые части уравнений (10.1) значениями не на левой, а на правой границе каждого шага:
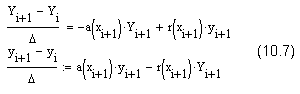
Граничные условия, конечно, можно оставить в том же виде (10.5). Поскольку мы имеем дело с линейными дифференциальными уравнениями, то и схему (10.7) легко будет записать в виде матричного равенства (10.6), перегруппировывая соответствующим образом выражение (10.7) и приводя подобные слагаемые. Разумеется, полученная матрица А будет иной, нежели матрица А для явной схемы (10.4). Поэтому и решение (реализация неявной схемы) может отличаться от изображенного на рис. 10.9 результата расчетов по явной схеме. Программа, составленная для решения системы (10.7), приведена в листинге 10.7.
Листинг 10.7. Реализация неявной разностной схемы для жесткой краевой задачи:

Не будем специально останавливаться на обсуждении листинга 10.7, поскольку он почти в точности повторяет предыдущий листинг. Отличие заключается лишь в формировании матрицы А другим способом, согласно неявной схеме. Решение, показанное на рис. 10.10, демонстрирует, что произошло "небольшое чудо": "разболтка" исчезла, а распределение интенсивностей стало физически предсказуемым. Обратите внимание, что (из-за взятого нами слишком большого коэффициента ослабления излучения) отраженный пучок света имеет очень маленькую интенсивность, и ее пришлось построить на графике с увеличением в тысячу раз.
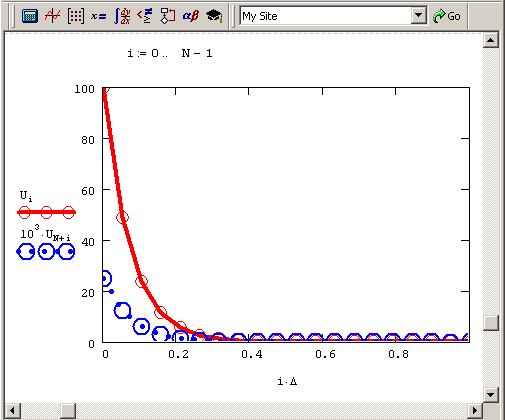
Рис. 10.10. Решение краевой задачи по неявной разностной схеме (продолжение листинга 10.7)
