Странный аттрактор
Одна из самых знаменитых динамических систем предложена в 1963 г. Лоренцем в качестве упрощенной модели конвективных турбулентных движений жидкости в нагреваемом сосуде тороидальной формы. Система состоит из трех ОДУ и имеет три параметра модели (листинг 9.15). Поскольку неизвестных функций три, то фазовый портрет системы должен определяться не на плоскости, а в трехмерном пространстве.
Листинг 9.15. Модель Лоренца:
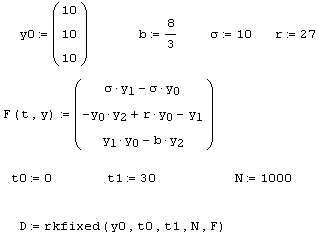
Решением системы Лоренца при определенном сочетании параметров (рис. 9.21 и 9.22) является странный аттрактор (или аттрактор Лоренца) – притягивающее множество траекторий на фазовом пространстве, которое по виду идентично случайному процессу. В некотором смысле аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника.
Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. В качестве примера на рис. 9.23 приведен результат для r=10 и тех же значений остальных параметров. Как видно, аттрактором в этом случае является фокус. Перестройка типа фазового портрета происходит в области промежуточных r. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описывает переход ламинарного движения жидкости к турбулентному.
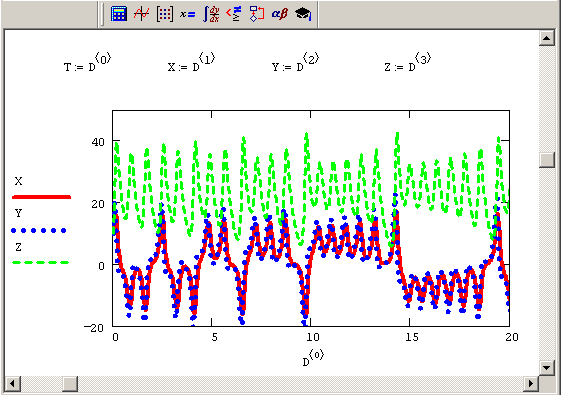
Рис. 9.21. Решение в виде аттрактора Лоренца (продолжение листинга 9.15)
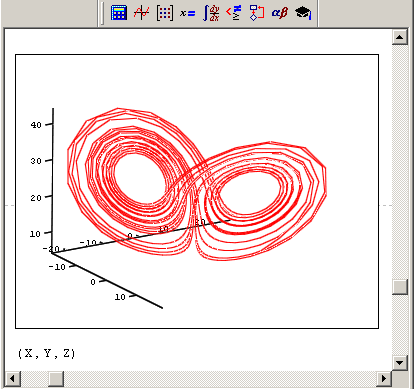
Рис. 9.22. Аттрактор Лоренца на фазовой плоскости (продолжение листинга 9.15)
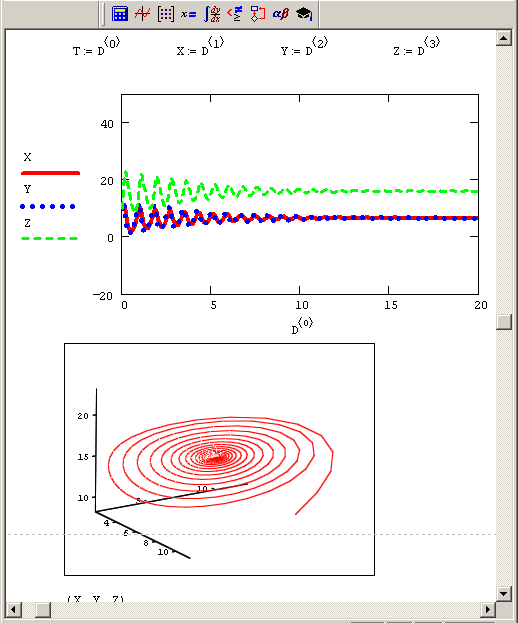
Рис. 9.23. Решение системы Лоренца с измененным параметром г=10
Замечательно, что решение подобных нелинейных динамических систем можно получить только численно, поэтому их изучение стало бурно развиваться с ростом возможностей вычислительной техники в последние полвека.
