Решение систем ОДУ в одной заданной точке
Зачастую при решении дифференциальных уравнений требуется определить значения искомых функций не на всем интервале (t0,t1), а только в одной его последней точке. Например, весьма распространены задачи поиска аттракторов динамических систем. Известно, что для широкого класса ОДУ одна и та же система при разных (или даже любых, как рассмотренный выше пример осциллятора с затуханием) начальных условиях при t › ∞ приходит в одну и ту же точку (аттрактор). Поэтому часто нужно определить именно эту точку.
Такая задача требует меньше ресурсов компьютера, чем решение системы ОДУ на всем интервале, поэтому в Mathcad имеются модификации встроенных функций Rkadapt и Buistoer. Они имеют несколько другой набор параметров и работают значительно быстрее своих аналогов:
- rkadapt (y0, t0, t1, асc, D, k, s) – метод Рунге-Кутты с переменным шагом;
- buistoer (y0,t0, t1,acc,D,k,s) – метод Булирша-Штера:
- y0 – вектор начальных значений в точке t0;
- t0,t1 – начальная и конечная точки расчета;
- асc – погрешность вычисления (чем она меньше, тем с лучшей точностью будет найдено решение; рекомендуется выбирать значения погрешности в районе 0.001);
- D – векторная функция, задающая систему ОДУ;
- k – максимальное число шагов, на которых численный метод будет находить решение;
- s – минимально допустимая величина шага.
Как легко заметить, вместо числа шагов на интервале интегрирования ОДУ в этих функциях необходимо задать точность расчета численным методом значения функций в последней точке. В этом смысле параметр асе похож на константу TOL, которая влияет на большинство встроенных численных алгоритмов Mathcad. Количество шагов и их расположение определяются численным методом автоматически, чтобы обеспечить эту точность. Два последних параметра нужны для того, чтобы пользователь мог искусственно повлиять на разбиение интервала на шаги. Параметр к служит для того, чтобы шагов не было чрезмерно много, причем нельзя сделать k>1000. Параметр s – для того, чтобы ни один шаг не был слишком малым для появления больших погрешностей при разностной аппроксимации дифференциальных уравнений внутри алгоритма. Эти параметры следует задавать явно, исходя из свойств конкретной системы ОДУ. Как правило, проведя ряд тестовых расчетов, можно подобрать их оптимальный набор для каждого конкретного случая.
Пример использования функции buistoer для той же модели линейного осциллятора приведен в листинге 9.5. В его первых двух строках, как обычно, определяется система уравнений и начальные условия; в следующей строке матрице и присваивается решение, полученное с помощью buistoer. Структура этой матрицы в точности такая же, как и в случае решения системы ОДУ посредством уже рассмотренных нами ранее встроенных функций (см. разд. 9.3.1). Однако в данном случае нам интересна только последняя точка интервала. Поскольку сделанное численным методом количество шагов, т. е. размер матрицы и, заранее неизвестно, то его необходимо предварительно определить. Это сделано в четвертой строке листинга, присваивающей это число переменной м, в этой же строке оно выведено на экран. В предпоследней строке листинга осуществлен вывод решения системы ОДУ на конце интервала, т. е. в точке t=s0 в виде вектора. В последней строке для примера еще раз выводится искомое значение первой функции из системы ОДУ (сравните его с соответствующим местом вектора из предыдущей строки). Чтобы попробовать альтернативный численный метод, достаточно в листинге 9.5 заменить имя функции buistoer на rkadapt.
Листинг 9.5. Поиск аттрактора системы двух ОДУ модели осциллятора:
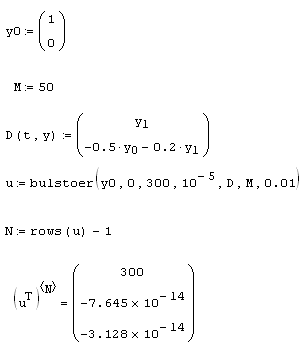
Внимание!
Функции bulstoer и rkadapt (те, что пишутся со строчной буквы) не предназначены для нахождения решения в промежуточных точках интервала, хотя они и выдают их в матрице-результате.