Система N дифференциальных уравнений. Встроенные функции для решения систем ОДУ.
При помощи Mathcad можно решать системы N>1 ОДУ первого порядка, если они записаны в стандартной форме (Коши) в виде векторного соотношения: Y' (t)=F(Y(t),t) (см. разд. 9.1. 1).
В Mathcad имеется несколько встроенных функций, которые позволяют решать задачу Коши различными численными методами. Для "хороших" нежестких систем ОДУ применяются следующие функции:
- rkfixed(y0, t0, t1,M,D) – метод Рунге-Кутты с фиксированным шагом;
- Rkadapt (y0,t0, t1,M,D) – метод Рунге-Кутты с переменным шагом;
- Buistoer(y0,t0,t0,M,D) – метод Булирша-Штера:
- у0 – вектор начальных значений в точке t0 размера NXI;
- t0 – начальная точка расчета;
- t1 – конечная точка расчета;
- M – число шагов, на которых численный метод находит решение;
- D – векторная функция размера Nx1 двух аргументов – скалярного t и векторного у. При этом у – искомая векторная функция аргумента t того же размера Nx1.
Внимание!
Соблюдайте регистр первой буквы рассматриваемых функций, поскольку это влияет на выбор алгоритма счета, в отличие от многих других встроенных функций Mathcad, например, Find=find (см. разд. 9.3.2).
Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)х(N+1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах – значения искомых функций y0(t),y1(t),…,yN-i(t), рассчитанные для этих значений аргумента (рис. 9.5). Поскольку всего точек (помимо начальной) м, то строк в матрице решения будет всего M+1.
В листинге 9.3 приведен пример решения той же самой системы ОДУ осциллятора с затуханием (см. разд. 9.1 и 9.2) при помощи первой из функций rkfixed. Результат расчетов представлен на рис. 9.5 как содержимое матрицы и на рис. 9.6 в виде графика. Точки, в которых получено решение, отмечены на графике рис. 9.6 кружками. Чтобы использовать другой численный алгоритм, достаточно поменять имя функции rkfixed в последней строке листинга на другое (на практике как раз более эффективны функции Rkadapt и Bulstoer).
Листинг 9.3. Решение системы двух ОДУ (модель осциллятора):
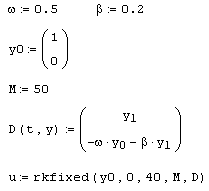

Рис. 9.5. Результат, выдаваемый встроенной функцией в качестве решения системы ОДУ (продолжение листинга 9.3}
