Пример: химическая кинетика
Рассмотрим классическую модель химической кинетики (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.
Попытка решения стандартными методами
Рассмотрим составную схему химического взаимодействия трех веществ. Пусть вещество "О" медленно превращается в "1": "0 " › "1 " (со скоростью 0.1), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2": "1"+"1 " › "2"+"1" (103). И, наконец, подобным образом (но со средней скоростью) реагируют вещества "2" и "1": "1"+"2" › "0" + "2" (102). Система ОДУ, описывающая динамику концентрации реагентов, с попыткой решения методом Рунге-Кутты, приведена, в символической форме в первой строке листинга 9.10.
Листинг 9.10. Жесткая система ОДУ химической кинетики:
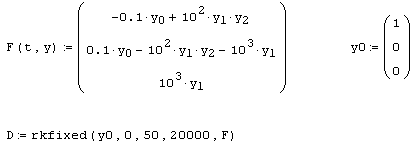
Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд 3.4.3). Чем сильнее вырождена матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях у0, y1 и у2 (листинг 9.11, вторая строка). В первой строке листинга 9.11 приведено напоминание способа вычисления якобиана средствами Mathcad на примере определения элементов его первой строки.
Листинг 9.11. Якобиан рассматриваемой системы ОДУ химической кинетики:
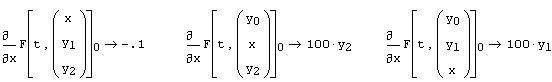
Для примера, приведенного в листинге 9.10, стандартным методом Рунге-Кутты все-таки удается найти решение (оно показано на рис. 9.15). Однако для этого требуется очень большое число шагов, M=20000, что делает расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. В процессе работы алгоритма оно расходится, и Mathcad вместо результата выдает ошибку о превышении предельно большого числа.
Еще один факт, на который стоит обратить внимание, – это различие в порядке величины получающегося решения. Как видно из рис. 9.15, концентрация первого реагента у1 существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жестких систем.
Примечание
В принципе, можно было бы снизить жесткость системы "вручную", применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию у1 к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие y1, на 1000. После масштабирования для решения полученной системы методом Рунге-Кутты будет достаточно взять всего м=20 шагов.
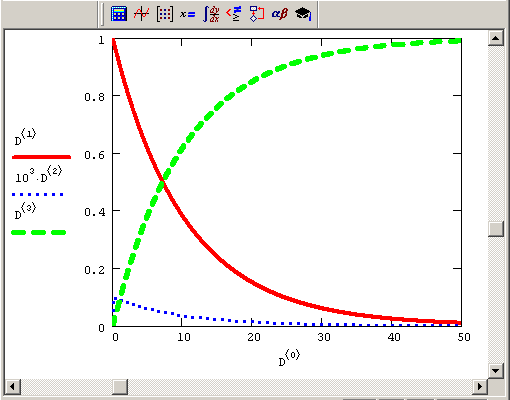
Рис. 9.15. Решение жесткой системы ОДУ химической кинетики методом Рунге-Кутты (продолжение листинга 9.10)