Иллюстрированный самоучитель по MathCAD 12

Пример: химическая кинетика

Применение специфических алгоритмов

Покажем действие этих алгоритмов на том же примере жесткой системы ОДУ химической кинетики (листинг 9.12). Обратите внимание, как следует представлять в данном случае якобиан, сравнив задание матричной функции в предпоследней строке листинга 9.12 с заданием якобиана из листинга 9.11.

Листинг 9.12. Решение жесткой системы ОДУ химической кинетики:

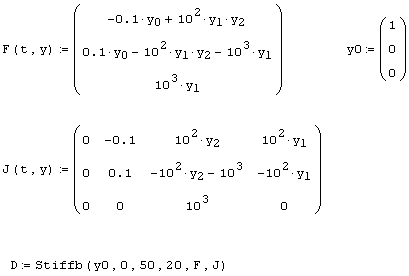
Расчеты показывают, что для получения того же результата (который был изображен на рис. 9.15) оказалось достаточно в тысячу раз меньшего количества шагов численного алгоритма, чем для стандартного метода Рунге-Купы! Примерно во столько же раз требуется меньше компьютерного времени на проведение расчетов. Стоит ли говорить, что, если вы имеете дело с жесткими (в той или иной степени) системами, применение описанных специальных алгоритмов просто необходимо.

Важно заметить, что до сих пор мы имели дело с примером не очень жесткой системы. Попробуйте вместо скоростей упомянутых химических реакций 0.1, 10³ и 10² взять другие числа, например, 0.05, 10⁴ и 10⁷ соответственно. Заметим, что такое соотношение скоростей часто встречается в прикладных задачах химической кинетики и определяет куда более жесткую систему ОДУ. Ее уже никак не удается решить стандартными методами, поскольку число шагов численного метода должно быть просто гигантским. А между тем алгоритмы для жестких ОДУ справляются с этой задачей с легкостью (рис. 9.16), причем практически при тех же значениях шага, что были взяты в листинге 9.12. Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 9.16 различаются еще сильнее, чем в предыдущем (менее жестком) примере.

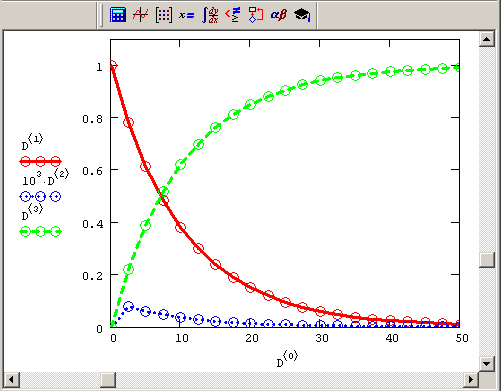
Рис. 9.16. Решение более жесткой системы ОДУ химической кинетики методом Розенброка

Для решения очень жестких систем особенно подходит функция Radau, которая соблазнительна еще и тем, что избавляет от необходимости предварительного расчета якобиана. В случае очень жесткой задачи химической кинетики результат, выдаваемый функцией Radau, практически тот же, что и в случае использования алгоритма Розенброка (рис. 9.16). Любопытно, что решение менее жесткой системы (из предыдущего листинга) при помощи функции Radau удается получить только для первой половины интервала, примерно до t1=20. Для больших интервалов она дает сбой, выводя вместо решения сообщение об ошибке.