О численных методах
Погрешность алгоритмов решения ОДУ в точке
Обратимся теперь к функциям buistoer и rkadapt (тем, что пишутся со строчной буквы), которые предназначены для нахождения решения в определенной точке интервала интегрирования системы ОДУ. В первую очередь, подчеркнем еще раз, что их нельзя применять для получения решения в промежуточных точках интервала, несмотря на их вывод в матрице-результате. На рис. 9.10 показан фазовый портрет системы ОДУ динамической модели осциллятора, полученный при помощи функции buistoer в листинге 9.5 (см. разд. 9.3.3) и с помощью rkadapt (при соответствующей замене третьей строки листинга 9.5). Видно, что, несмотря на высокую точность, равную 10-5, и верный результат на конце интервала, график, полученный при помощи функции buistoer (рис. 9.10, а), мало напоминает правильный фазовый портрет (см. рис. 9.9), начиная быть приемлемым только при предельно допустимом для обсуждаемых функций значении асс=10-16. В данном случае конкретной системы ОДУ функция rkadapt дает качественно верное решение (рис. 9.10, б), однако его необходимая точность обеспечивается только в последней точке временного интервала.
В заключение остановимся на влиянии выбора параметра асе на расчеты. Как правило, разные численные методы работают несколько по-разному. Алгоритм Рунге-Кутты дает результат тем ближе к истинному, чем меньше выбирается параметр асе, а Булирша-Штера часто демонстрирует менее естественную зависимость у(е): даже при относительно больших е реальная погрешность остается хорошей (намного лучше метода Рунге-Кутты).
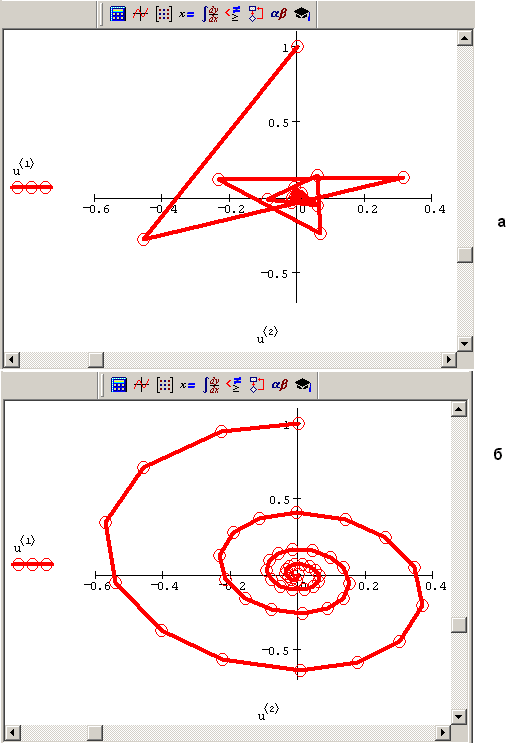
Рис. 9.10. Фазовый портрет, полученный bulstoer (a) и rkadapt (б) (продолжение листинга 9.5)
Поэтому для экономии времени расчетов в функции buistoer можно выбирать и большие асе.
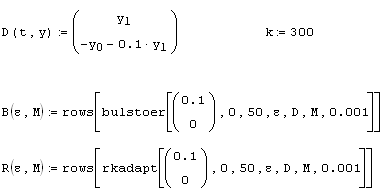
Чтобы обеспечить заданную точность, данные алгоритмы могут изменять как количество шагов, разбивающих интервал (t0,t1), так и их расположение вдоль интервала. Чтобы выяснить, на сколько шагов разбивался интервал при расчетах, воспользуемся простой программой, представленной в листинге 9.7. В ней определены пользовательские функции R(е) и B(е), вычисляющие для конкретной задачи (методов Рунге-Кутты и Булирша-Штера соответственно) зависимость числа шагов (т. е. числа строк получающейся матрицы) от параметра е=асс. Графики функций R(e) и B(е) показаны на рис. 9.11. Как видно, методу Рунге-Кутты при увеличении требуемой точности требуется все возрастающее количество шагов (и, соответственно, времени на расчеты), в противоположность методу Булирша-Штера, демонстрирующему большую экономичность.
Примечание
Максимальное количество шагов алгоритма ограничивается еще одним параметром k встроенных функций buistoer и rkadapt (см. разд. 9.3.3).
Листинг 9.7. Число шагов адаптивного численного алгоритма в зависимости от погрешности acc:
Таким образом, проводя тестовые расчеты для различных задач и подбирая наилучший набор параметров, можно существенно сэкономить ресурсы компьютера. Конечно, проводить подобный анализ стоит в случаях, когда время расчетов для вас критично.
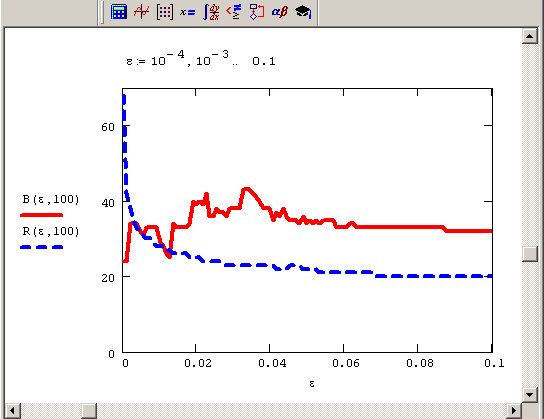
Рис. 9.11. Зависимость числа шагов от параметра асе численных методов (продолжение листинга 9.7)
