Примеры: классические динамические системы. Модели динамики биологических популяций.
В предыдущих разделах было использовано в качестве примера в основном линейное уравнение осциллятора (оно содержало только первую степень неизвестных функций и их производных). Между тем многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение большинства из них можно получить лишь численно.
Рассмотрим несколько наиболее известных классических примеров динамических систем, имея в виду, что читателю они могут пригодиться как в познавательных, так и в практических целях. Это модели динамики популяций (Вольтерры), генератора автоколебаний (Ван дер Поля), турбулентной конвекции (Лоренца) и химической реакции с диффузией (Пригожина). Как уже было сказано, для изучения динамических систем разработана специальная теория, центральным моментом которой является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.
Примечание
В большинстве примеров, изложенных ниже, для построения схемы фазового портрета рассчитывается несколько решений для разных начальных условий. О, том, как проделать такие расчеты в Mathcad, будет рассказано ниже на примере модели брюсселятора (см. разд. 9.5.4).
Ограничимся в дальнейшем минимальными комментариями и приведем листинги и графики решений без подробного обсуждения.
Модели динамики биологических популяций
Модель взаимодействия "хищник-жертва" независимо предложили в 1925-1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения (листинг 9.13) моделируют временную динамику численности двух биологических популяций жертвы у0 и хищника у1 Предполагается, что жертвы размножаются с постоянной скоростью с, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r), и умирают естественным образом (смертность определяется константой 0). В листинге рассчитываются три решения D, G, P для разных начальных условий.
Листинг 9.13. Модель "хищник-жертва":
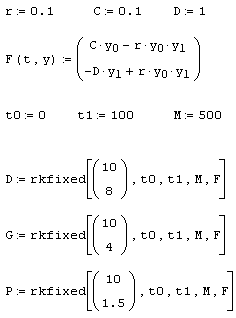
Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника (рис. 9.17), и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий – после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Примечание
Пример негрубой системы (модель осциллятора без затухания) с особой точкой типа "центр" был нами рассмотрен ранее (см. разд. 9.1).
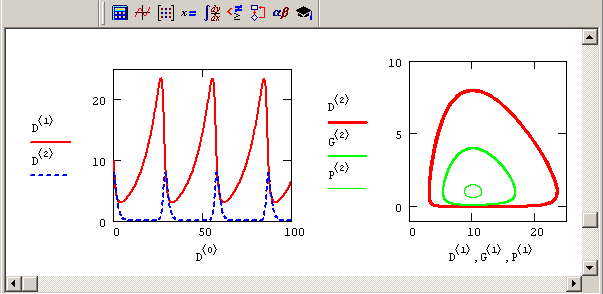
Рис. 9.17. График решения (слева) и фазовый портрет (справа) системы "хищник-жертва" (продолжение листинга 9.13)
Рассмотренную модель динамики двух популяций легко можно модифицировать, изменив тип взаимодействия "хищник-жертва" на тип конкуренции. Для этого надо учесть, что рост численности каждой популяции тормозит, во-первых, межвидовая, и, во-вторых, внутривидовая конкуренция.
В результате система (во второй строке листинга) запишется в виде:
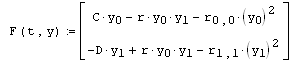
Где матрица r задает коэффициенты убывания численности вследствие конкурентной борьбы (диагональные элементы соответствуют внутри-, а недиагональные – межвидовой конкуренции).
График решения (для разных начальных условий) и фазовый портрет для описанной системы ОДУ показаны на рис. 9.18. Как видно, конкурентная борьба приводит к установлению некоторого стационарного состояния, выражающего равновесие видов. Особая точка, к которой стремится решение системы ОДУ подобным образом, называется узлом.
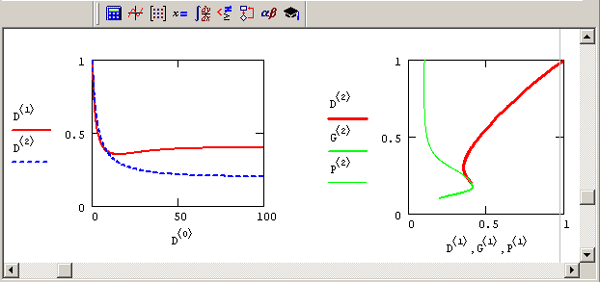
Рис. 9.18. График решения (слева) и фазовый портрет (справа) модели конкуренции популяций
