Жесткие системы ОДУ
До сих пор мы имели дело с "хорошими" уравнениями, которые надежно решались численными методами Рунге-Кутты. Однако имеется класс так называемых жестких (stiff) систем ОДУ, для которых стандартные методы практически неприменимы, поскольку их решение требует исключительно малого значения шага численного метода. Некоторые из специальных алгоритмов, разработанных для этих систем, реализованы в Mathcad.
Что такое жесткие ОДУ?
Исторически интерес к жестким системам возник в середине XX в. при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций (оно будет рассмотрено в разд. 9.4.3). Тогда неожиданно оказалось, что считавшиеся исключительно надежными методы Рунге-Кутты стали давать сбой при расчете этих задач.
Строгого общепринятого математического определения жестких ОДУ нет. В рамках этой книги будем считать, что жесткие системы – это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов (типа тех, что были рассмотрены в предыдущих разделах). Примерно такое определение было предложено в 1950-х гг. классиками в этой области Кертиссом и Хиршфельдером. Начнем разговор о жестких ОДУ с примера нежесткого уравнения (листинг 9.8), решение которого удается получить численным методом Рунге-Кутты (рис. 9.12).
Листинг 9.8. Решение нежесткого ОДУ:
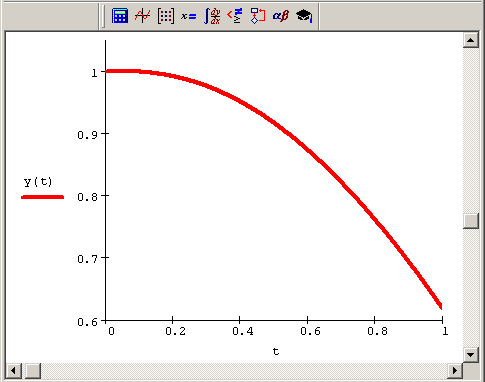
Рис. 9.12. Решение нежесткого ОДУ методом Рунге-Кутты (продолжение листинга 9.8)
Обратите внимание на значение коэффициента -10 во второй строке листинга. Если изменить его на -50, то решение меняется до неузнаваемости (рис. 9.13). Вас, несомненно, должен насторожить результат, выданный Mathcad. Характерная "разболтка" решения говорит о неустойчивости алгоритма. Первое, что можно сделать, – увеличить количество шагов в методе Рунге-Куттты. Для этого достаточно добавить третий параметр step в функцию odesoive (t, i,step). После нескольких экспериментов можно подобрать такое значение step, которое будет обеспечивать устойчивость решения. Читатель может самостоятельно убедиться, что при step>50 "разболтка" пропадает, и решение принимает вид графика, показанного ниже на рис. 9.14.
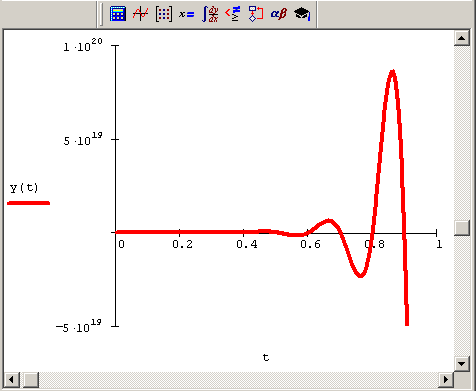
Рис. 9.13. Неверное решение более жесткого ОДУ методом Рунге-Кутты (листинг 9.8 с коэффициентом -50)
Таким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 9.8 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.
Примечание
Некоторые ученые замечают, что в последние годы методы Рунге-Кутты, считавшиеся ранее незыблемыми, стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.