О постановке задач. Задачи Коши для ОДУ.
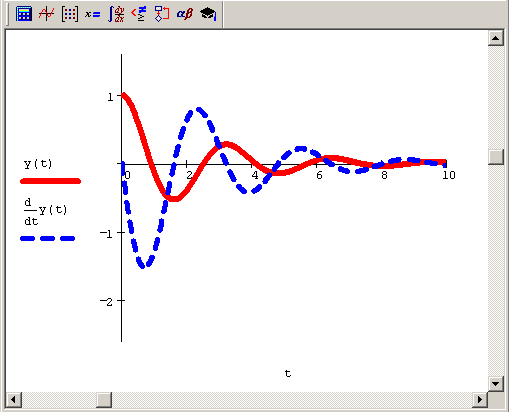
Рис. 9.1. Решение уравнения w2 у"+βу'+у=0 (продолжение листинга 9.1)
Имеются два типа задач, которые возможно решать с помощью Mathcad:
- задачи Коши – для которых определены начальные условия на искомые функции, т. е. заданы значения этих функций в начальной точке интервала интегрирования уравнения (именно им и посвящена данная глава);
- краевые задачи – для которых заданы определенные соотношения сразу на обеих границах интервала (они рассматриваются в главе 10).
Сказанное относится как к отдельным дифференциальным уравнениям (см. разд. 9.2), так и к системам ОДУ (см. разд. 9.3). Важно подчеркнуть, что Mathcad умеет решать только такие системы дифференциальных уравнений, которые могут быть представлены в стандартной форме (форме Коши). Для неизвестных функций у0 (t), y1(t),…, yN-1(t) система ОДУ должна быть записана в форме:
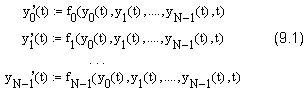
Что эквивалентно следующему векторному представлению:
Y'(t) = F(Y(t), t), (9.2)Здесь Y и Y' – соответствующие неизвестные векторные функции переменной t размера Nx1, а F – векторная функция того же размера и количества переменных (N+1) (N компонент вектора и, возможно, t). Именно векторное представление (9.2) используется для ввода системы ОДУ в среде Mathcad.
Для того чтобы определить задачу Коши для системы из N ОДУ первого порядка, следует определить еще ровно N начальных условий, задающих значение каждой из функций yi(t0) в начальной точке интегрирования системы t0. В векторной форме они могут быть записаны в виде:
Y(t0) = B, (9.3)Где B – вектор начальных условий размера Nx1, составленный из yi(t0). Обратите внимание на необходимость векторной записи как самого уравнения, так и начального условия. В случае одного ОДУ первого порядка соответствующие векторы имеют только один элемент, а в случае системы N>1 уравнений – N.
Стандартные процедуры Mathcad применимы для систем ОДУ первого порядка, записанных в форме (9.2)– (9.3). Тем не менее, если в систему входят и уравнения высших порядков, то ее можно свести к системе большего числа уравнений первого порядка. Рассмотрим в качестве примера уравнение второго порядка модели осциллятора w2 у'+βу'+у=0, решенное в листинге 9.1. Если ввести обозначение y0(t)=y(t), yi(t)=y' (t), то уравнение сведется к эквивалентной системе:
y0(t)=y1(t);
w2 у1'+βу'+у=0,
Форма которой удовлетворяет форме (9.2) и уравнение может быть решено средствами Mathcad, предназначенными для систем ОДУ. Именно эта система решена ниже в листинге 9.3 (см. разд. 9.3.1). Отметим, что на рис. 9.1 показаны как зависимость у (t), так и у1 (t)=y' (t).
