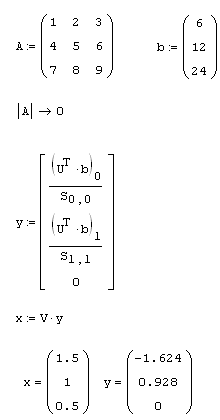Иллюстрированный самоучитель по MathCAD 12

SVD-(сингулярное) разложение

Наиболее эффективными (но и ресурсоемкими) средствами решения произвольных СЛАУ (с матрицей А размера NxM) по методу наименьших квадратов являются так называемые полные ортогональные разложения, имеющие, по определению, вид A=UKV^T.

Здесь U и V – ортогональные матрицы размером NxN и MхM соответственно, а k – матрица размера NxM, имеющая следующую структуру:

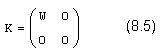
Причем w – матрица размера kxk, где k – ранг исходной матрицы А.

Самое известное из ортогональных, SVD-(singular value decomposition) или сингулярное разложение – разложение вида A=USV^T, где S – диагональная матрица, состоящая из нулей и расположенных на диагонали сингулярных чисел матрицы А. Расчет сингулярного разложения в Mathcad осуществляется при помощи пары встроенных функций:

• svds (A) – вектор, состоящий из сингулярных чисел;
• svd (A) – сингулярное разложение:
  • А – действительная матрица.

Пример поиска сингулярного разложения сингулярной матрицы приведен в листинге 8.25, причем его последняя строка представляет собой проверку правильности найденного разложения. Подчеркнем, что вычисленные сингулярные числа находятся на главной диагонали средней матрицы разложения, а ее остальные элементы, по определению, равны нулю. Сравнивая матрицы из листинга 8.25, вы без труда разберетесь, каким образом следует выделять искомые матрицы сингулярного разложения из результата, поставляемого функцией svd.

Листинг 8.25. Сингулярное разложение сингулярной матрицы:

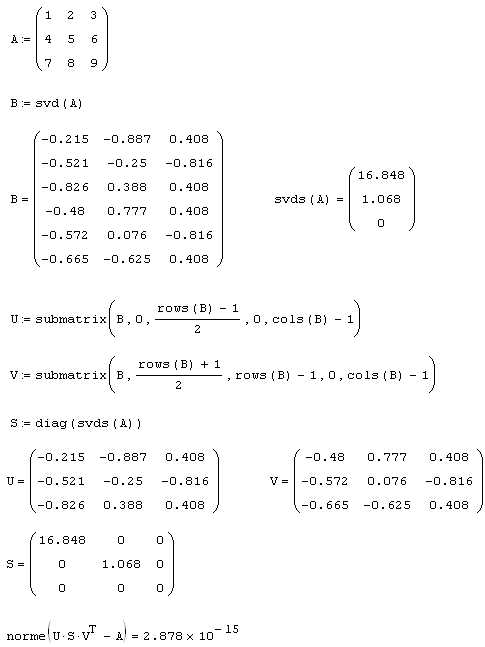
Венцом современных алгоритмов решения произвольных СЛАУ является SVD-разложение. Прежде чем прокомментировать соответствующий алгоритм, приведенный в листинге 8.26, обратим внимание на матрицу S, которая имеет блочную структуру. Согласно формуле (8.5), из матрицы s можно выделить подматрицу w с ненулевыми диагональными элементами. Дальнейшая последовательность действий по построению нормального псевдорешения выглядит так:

1. Нахождение единственного решения вспомогательной СЛАУ: Wy=U^T b (первые два элементы вектора у во второй строке листинга 8.26, которая учитывает диагональность матрицы S).
2. Дополнение вектора нулевыми элементами до размера искомого вектора х.
3. Вычисление х простым умножением x=Vy (третья строка листинга).

Полученный результат (искомый вектор х и промежуточный у) выведен в конце листинга 8.26. Как вы можете убедиться, он совпадает с ответом, полученным в листинге 8.24 (см. предыдущий разд.) при помощи QR-разложения.

Листинг 8.26. Решение вырожденной СЛАУ при помощи сингулярного разложения (продолжение листинга 8.25):