Произвольные системы линейных уравнений. Переопределенные системы.
Классические задачи решения СЛАУ, рассмотренные в предыдущем разделе, предполагают равное количество уравнений и неизвестных, т. е. квадратную матрицу А. Именно для таких систем доказано, что решение существует и единственно, если определитель матрицы |А| #0. Рассмотрим теперь задачи, в которых матрица А не является квадратной либо плохо обусловлена. Разберемся в этом разделе лишь с основными свойствами и идеологией подхода к таким системам, имея в виду, что наиболее эффективными способами их решения являются матричные разложения (см. разд. 8.3).
Начнем разговор о "плохих" СЛАУ с переопределенными условиями, в которых число уравнений больше числа неизвестных.
О постановке задач
Чаще всего СЛАУ с прямоугольной матрицей размера MxN (при M>N, т. е. при числе уравнений большем числа неизвестных) вовсе не имеет решения, т. е. является несовместной, или переопределенной. Листинг 8.6 демонстрирует, что несовместные системы не могут быть решены ни при помощи встроенной функции isolve, ни посредством вычислительного блока Given/Find.
Листинг 8.6. Попытка решения несовместных СЛАУ:
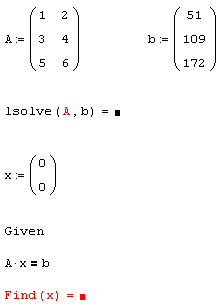
Примечание
Конечно, в редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор b), как это показано в листинге 8.7. Любопытно, что итерационный алгоритм блока Given/Find справляется с такой задачей, а алгоритм исключения, заложенный в функции Isolve, – нет.
Листинг 8.7. Пример нахождения решения СЛАУ с прямоугольной матрицей:
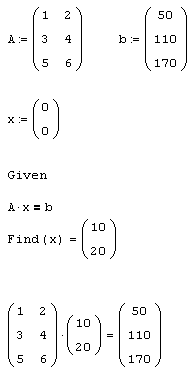
На практике (особенно в последнее время) задачи отыскания решения переопределенных СЛАУ встречаются довольно часто. Приведем простую интерпретацию переопределенной задачи, связанной с обработкой результатов какого-либо эксперимента, например, взвешивания предметов двух типов (для простоты и определенности, совершенно одинаковых яблок и одинаковых груш). Если, согласно постановке задачи, на весы можно положить любое количество предметов любого типа, то модель каждого акта взвешивания представится линейным уравнением, двумя неизвестными в которых будет масса яблока и масса груши. Очевидно, что чем больше взвешиваний мы проведем, тем точнее (в условиях присутствующей в эксперименте погрешности измерений) сможем определить искомые величины.
Обращаясь к числовым примерам листингов 8.6 и 8.7, легко сообразить, что они соответствуют трем актам взвешивания, когда в первый раз на весы кладется одно яблоко и две груши, во второй – три яблока и четыре груши, и в третий – пять яблок и шесть груш. Листинг 8.7 может описывать случай, когда погрешность эксперимента полностью отсутствует, и система трех уравнений с двумя неизвестными оказывается совместной. А листинг 8.6 является примером куда более типичной ситуации, когда погрешность каждого измерения приводит к тому, что итоговая СЛАУ оказывается несовместной, т. е. не имеет никакого точного решения.
Примечание
Простой пример с яблоками и грушами является типичным представителем класса обратных задач, подразумевающих, в частности, восстановление неизвестных входных данных эксперимента по наблюдаемым выходным характеристикам (получаемым в условиях наличия погрешности). Для таких задач развиты специальные методы решения, наиболее простой из которых мы приводим в этом и следующем разделах (не останавливаясь на его обосновании, которое потребовало бы привлечения дополнительных соображений из области математической статистики).