Произвольные системы линейных уравнений. Переопределенные системы.
Псевдорешение (метод наименьших квадратов)
Напрашивающийся сам собой путь решения нашего простого примера с грушами и яблоками является хорошей иллюстрацией подхода к общей проблеме переопределенных СЛАУ. А именно, вместо точного решения системы уравнений следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т. е. минимизировать их невязку (расхождение между вектором Aх и вектором правой части СЛАУ b). Поскольку невязка Аx-b является векторной величиной, то, исходя из практических соображений, минимизации надо подвергать ее норму (т. е. скаляр) |Аx-b|. Этот подход позволит, с одной стороны, получить разумное, с физической точки зрения, решение задачи, а, с другой – использовать полезную информацию, заключенную во всех уравнениях.
Таким образом, при интерпретации переопределенных СЛАУ принято искать не точное решение (которого, как уже отмечалось, при данной постановке задачи просто нет), а псевдорешение – вектор, минимизирующий норму невязки системы уравнений. Таким образом, задача решения линейной системы уравнений заменяется задачей отыскания глобального минимума функции f (x) = |Аx-b|. Повторимся еще раз, что, в полном соответствии с обозначениями, принятыми в Mathcad, х – это неизвестный вектор, а символ модуля (две вертикальные черты) означает операцию вычисления нормы (евклидовой длины вектора). Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является ни чем иным, как реализацией метода наименьших квадратов (МНК).
График функции двух переменных f(x0,x1) показан в виде трехмерной поверхности на рис. 8.1, а несколько его сечений в окрестности минимума – на рис. 8.2. Нетрудно сообразить, почему структура функции оказывается именно такой, если вспомнить, что f(x)2 является квадратичной формой относительно неизвестных х0 и x1 Надо отметить, что если бы наша система имела большее число уравнений, то вычислительная задача соответствующим образом усложнилась бы, т. к. минимизацию следовало бы проводить не по двум, а по большему числу переменных.

Рис. 8.1. График минимизируемой функции невязки f (х) = | Ах-b|
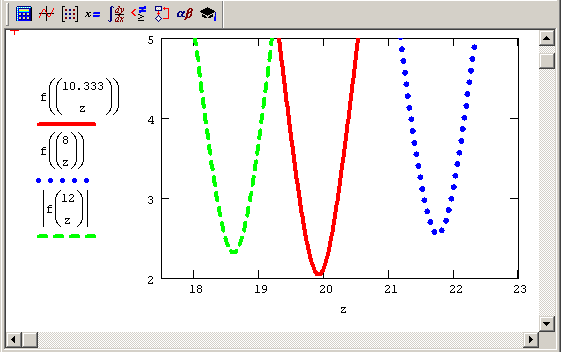
Рис. 8.2. Сечения графика невязки f (х) для трех фиксированных значений х0
