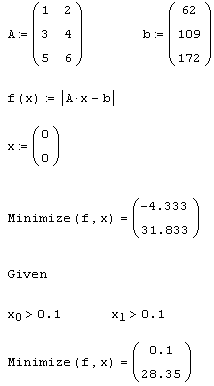Произвольные системы линейных уравнений. Переопределенные системы.
По умолчанию решение линейной системы уравнений производится при помощи линейного алгоритма. Чтобы сменить его на нелинейный, необходимо нажатием правой кнопки мыши вызвать из области имени функции контекстное меню и сменить тип метода Linear (Линейный) на один из нелинейных методов Nonlinear (Нелинейный) (рис. 8.3). Однако даже в этом случае, как показывает опыт, наиболее правильный ответ получается только для одного из трех доступных численных алгоритмов.
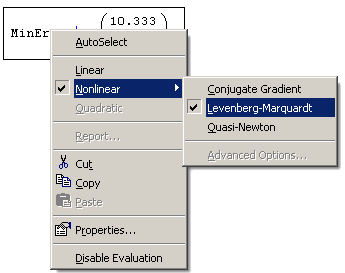
Рис. 8.3. Изменение численного алгоритма для функции Minerr
Во-вторых, приближенное решение СЛАУ посредством вычислительного блока Given/Minerr невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В частности, математически более правильным было решать нашу задачу о яблоках и грушах с дополнительным условием положительной определенности компонент неизвестного вектора (поскольку масса фруктов по определению больше нуля). В результате исходная задача сводится к условной минимизации функции f (х), что в Mathcad-программе соответствует появлению дополнительных неравенств после ключевого слова Given (см. пример ниже, решенный в листинге 8. 10). Однако все уравнения и неравенства, предшествующие функции Minerr, будут восприниматься численным процессором Mathcad одинаково, т. е. не в качестве жестких условий, а как выражения, которые должны выполняться лишь с некоторой точностью. В результате найденное решение может вовсе не отвечать условию положительной определенности (этот вопрос обсуждался в разд. 6.2, когда речь шла о задачах оптимизации).
В свете перечисленных проблем применение функции Minimize для поиска псевдорешения СЛАУ выглядит более обоснованным. К слову заметим, что выбор любого из трех нелинейных численных алгоритмов минимизации приводит к одинаковым результатам (листинг 8.9). Функция Minimize годится и для отыскания псевдорешения с дополнительными условиями, выражающими имеющуюся априорную информацию. Соответствующий пример иллюстрирует листинг 8.10, в котором осуществляется поиск псевдорешения СЛАУ, немного отличающейся от рассмотренной выше. Это отличие приводит к тому, что при использовании той же самой методики получается отрицательное решение (третья строка листинга). При добавлении в задачу дополнительных условий результат минимизации оказывается другим (последняя строка листинга 8.10).
Примечание
Несколько иной подход к переопределенным системам, для которых имеется дополнительная информация другого типа (а именно, априорная оценка неизвестного вектора х), будет изложен в следующем разделе.
Листинг 8.10. Поиск псевдорешения при наличии априорной информации:
