Недоопределенные системы
Нормальное псевдорешение
Способ выбора одного решения из бесконечного множества, изображенного на рис. 8.4, подсказывает, по аналогии с переопределенными СЛАУ (см. разд. 8.2. Т), сам физический смысл задачи, которую можно интерпретировать как м измерений с N неизвестными (M<N). Для того чтобы получить разумное единственное решение задачи, необходимо "доопределить" ее, добавив некоторые априорные соображения о значении неизвестного вектора х.
Если априорной информации о примерной величине вектора х нет, единственным образом решить СЛАУ невозможно. Однако если о неизвестном векторе хоть что-то можно сказать, данная информация позволит доопределить систему уравнений и получить решение, учитывающее как систему, так и априорную информацию. Иными словами, следует ввести в задачу определенные ожидания о величине вектора х. Математически, не теряя общности, можно полагать ожидаемое значение вектора х нулевым, поскольку перейти от любого х к нуль-вектору можно простым линейным преобразованием переменных, которое изменит только вектор правой части b.
Таким образом, вполне логично объявить решением недоопределенной СЛАУ такое из решений, которое ближе всего находится к нулевому вектору, т. е. обладает минимальной нормой |х| -min. Это решение называют нормальным псевдорешением СЛАУ, и искать его следует, минимизируя норму вектора х на предварительно полученном семействе решений СЛАУ. Иными словами, решение недоопределенной СЛАУ сводится к условной минимизации функции |х| (рис. 8.5). Геометрический смысл нормального псевдорешения (в рассматриваемом случае одного уравнения с двумя неизвестными) очевиден: это точка, лежащая на пересечении прямой семейства всех решений и перпендикуляра к этой прямой, восстановленного из начала координат. На рис. 8.4 нормальное псевдорешение выделено пунктирными линиями.
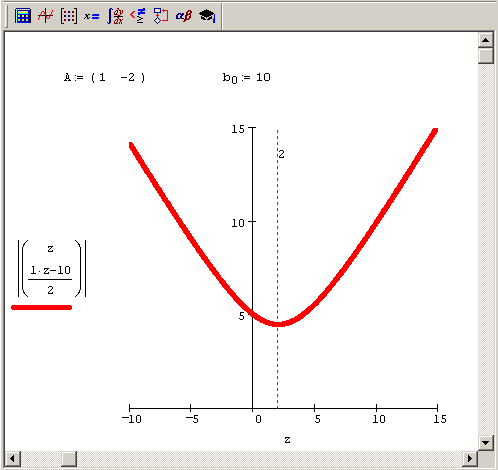
Рис. 8.5. График функции f (x0) = |х| при условии, что xc-2xi=10
Принимая во внимание введенную технику решения недоопределенных СЛАУ, можно предложить для этих задач простой и понятный алгоритм, опирающийся на встроенную функцию Minimize. В листинге 8.12 решена задача численного отыскания псевдорешения рассматриваемого единственного уравнения (рис. 8.5), а в листинге 8.13 – решение недоопределенной системы двух уравнений с тремя неизвестными, которая исследовалась аналитически в листинге 8.11 (см. предыдущий разд.). Как уже отмечалось, смысл обоих листингов заключается в минимизации нормы искомого вектора при условии, что выполнена система равенств Aх=b. Графики функции f (х) = |х|, при условии выполнения СЛАУ из листингов 8.12 и 8.13, изображены на рис. 8.5 и 8.6 соответственно.
