Недоопределенные системы
Листинг 8.12. Поиск нормального псевдорешения уравнения x0-2xi=10:
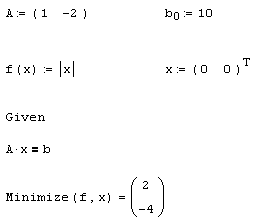
Примечание
Возвращаясь к примеру с грушами и яблоками (см. разд. 8.2), можно интерпретировать недоопределенную СЛАУ из листинга 8.12 как единственное измерение, которого недостаточно для однозначного определения веса одной груши и одного яблока. Однако если учесть априорную оценку об этих весах (пусть даже весьма грубую), это позволит отыскать решение, которое будет осмысленным. Конечно, в этом случае следует выбрать соответствующий вектор априорной оценки (в третьей строке листинга 8.12) и, кроме того, добавить дополнительное условие на положительную определенность неизвестных, как в листинге 8.10 (см. раза. 8.2.2).
Листинг 8.13. Поиск нормального псевдорешения недоопределенной СЛАУ:
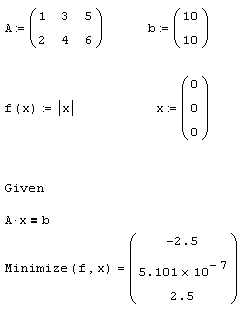
Примечание
Если недоопределенная СЛАУ не имеет бесконечного множества решений, а является несовместной, то способ, предложенный в листинге 8.13, использовать нельзя, т. к. условие заведомо невыполнимо. Подход к решению таких задач заключается в поиске компромиссного решения, минимизирующего как норму невязки, так и норму решения (см. разд. 8.2.3).
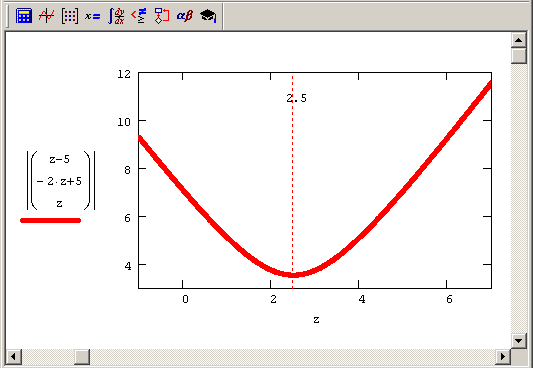
Рис. 8.6. График функции f (х2) = |х| при условии выполнения СЛАУ из листинга 8.13
