Вырожденные и плохо обусловленные системы
Вернемся вновь к СЛАУ Aх=b с квадратной матрицей А размера MхN, которая, в отличие от рассмотренного выше "хорошего" случая (см. разд. 8.Г), требует специального подхода. Обратим внимание на два похожих типа СЛАУ:
- вырожденная система (с нулевым определителем |А|=0);
- плохо обусловленная система (определитель А не равен нулю, но число обусловленности очень велико).
Несмотря на то, что эти типы систем уравнений существенно отличаются друг от друга (для первого решение отсутствует, а для второго существует и единственно), с практической точки зрения вычислителя, между ними много общего.
Вырожденные СЛАУ
Вырожденная система – это система, описываемая матрицей с нулевым определителем |A|=0 (сингулярной матрицей). Поскольку некоторые уравнения, входящие в такую систему, представляются линейной комбинацией других уравнений, то фактически сама система является недоопределенной. Несложно сообразить, что, в зависимости от конкретного вида вектора правой части ь, существует либо бесконечное множество решений, либо не существует ни одного. Первый из вариантов сводится к построению нормального псевдорешения (т. е. выбора из бесконечного множества решений такого, которое наиболее близко к определенному, например, нулевому, вектору). Данный случай был подробно рассмотрен в разд. 8.2.2 (см. листинги 8.11-8.13).
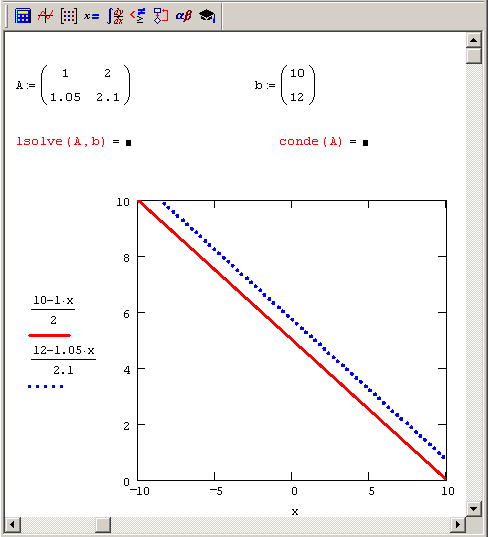
Рис. 8.7. Графическое представление несовместной системы двух уравнений с сингулярной матрицей
Рассмотрим второй случай, когда СЛАУ Aх=b с сингулярной квадратной матрицей А не имеет ни одного решения. Пример такой задачи (для системы двух уравнений) проиллюстрирован рис. 8.7, в верхней части которого вводятся матрица А и вектор b, а также предпринимается (неудачная, поскольку матрица А сингулярная) попытка решить систему при помощи функции isolve. График, занимающий основную часть рисунка, показывает, что два уравнения, задающие систему, определяют на плоскости (x0,x1) две параллельные прямые. Прямые не пересекаются ни в одной точке координатной плоскости, и решения системы, соответственно, не существует.
Примечание
Во-первых, заметим, что СЛАУ, заданная несингулярной квадратной матрицей размера 2x2, определяет на плоскости пару пересекающихся прямых (см. рис. 8.9 ниже). Во-вторых, стоит сказать, что, если бы система была совместной, то геометрическим изображением уравнений были бы две совпадающие прямые, описывающие бесконечное число решений.
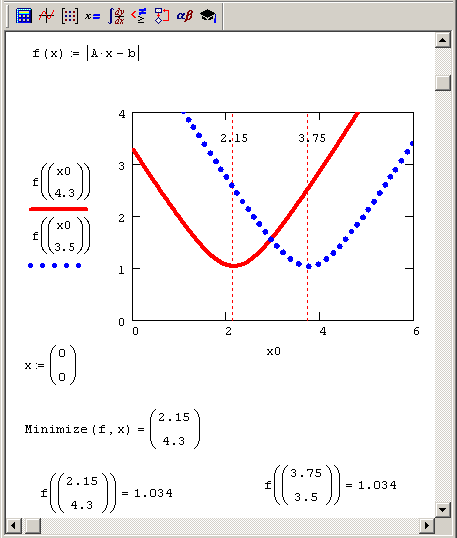
Рис. 8.8. График сечений функции невязки f (х) = |Ах-b|
Несложно догадаться, что в рассматриваемом сингулярном случае псевдорешений системы, минимизирующих невязку |Ax-b|, будет бесконечно много, и лежать они будут на третьей прямой, параллельной двум показанным на рис. 8.7 и расположенной в середине между ними. Это иллюстрирует рис. 8.8, на котором представлено несколько сечений функции f(x)= | Аx-b |, которые говорят о наличии семейства минимумов одинаковой глубины. Если попытаться использовать для их отыскания встроенную функцию Minimize, ее численный метод будет всегда отыскивать какую-либо одну точку упомянутой прямой (в зависимости от начальных условий). Поэтому для определения единственного решения следует выбрать из всего множества псевдорешений то, которое обладает наименьшей нормой. Можно пытаться оформить данную многомерную задачу минимизации в Mathcad при помощи комбинаций встроенных функций Minimize, однако более эффективным способом будет использование регуляризации (см. ниже) или ортогональных матричных разложений (см. разд. 8.3).
