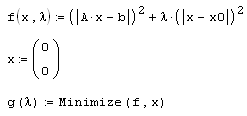Вырожденные и плохо обусловленные системы
Метод регуляризации
Для решения некорректных задач, в частности, вырожденных и плохо обусловленных СЛАУ, разработан очень эффективный прием, называемый регуляризацией. В его основе лежит учет дополнительной априорной информации о структуре решения (векторе априорной оценки хо), которая очень часто присутствует в практических случаях. В связи с тем, что регуляризация была подробно рассмотрена в разд. 6.3.3, напомним лишь, что задачу решения СЛАУ Аx=b можно заменить задачей отыскания минимума функционала Тихонова:
Ω(х,λ) = |Ах-b|2 +λ|х-х0|2. (8.3)
Здесь λ, – малый положительный параметр регуляризации, который необходимо подобрать некоторым оптимальным способом. Можно показать, что задачу минимизации функционала Тихонова можно, в свою очередь, свести к решению другой СЛАУ:
(АT А+λI)-х=АT В+λх0, (8.4)
Которая при λ › 0 переходит в исходную плохо обусловленную систему, а при больших x, будучи хорошо обусловленной, имеет решение х0. Очевидно, оптимальным будет некоторое промежуточное значение А, устанавливающее определенный компромисс между приемлемой обусловленностью и близостью к исходной задаче. Отметим, что регуляризационный подход сводит некорректную задачу к условно-корректной (по Тихонову) задаче отыскания решения системы (8.4), которое, в силу линейности задачи, является единственным и устойчивым.
Приведем, без излишних комментариев, регуляризованное решение вырожденной системы, которая была представлена на рис. 8.8. Листинг 8.15 демонстрирует отыскание решения задачи (8.4), а полученная зависимость невязки и самого решения от параметра регуляризации λ показана на рис. 8.11 и 8.12 соответственно. Важно подчеркнуть, что решения исходной системы и, следовательно, системы (8.4) при λ=0 не существует.
Листинг 8.15.Регуляризация вырожденной СЛАУ:
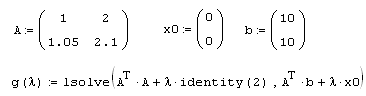
Заключительным шагом регуляризации является выбор оптимального λ. Имеется, по крайней мере, два соображения, исходя из которых, можно выбрать параметр регуляризации, если опираться на зависимость от него невязки. В рассматриваемом примере применим критерий определения λ, опирающийся – на подбор нормы невязки, равной априорной оценке погрешностей задания входных данных: матрицы А и вектора b, т. е. величине |δA| + |5λ|. Например, можно выбрать норму невязки и, соответственно, параметр λ и решение х(λ), которые отмечены на рис. 8.11 и 8.12 пунктирами.
Примечание 1
Другим вариантом выбора λ, не требующим никаких априорных соображений относительно погрешностей модели, является так называемый квазиоптимальный метод, рассмотренный в разд. 6.3.3.
Примечание 2
Полезно убедиться в том, что формула (8.4) в случае линейной задачи дает тот же результат, что и общая формула (8.3). Для этого достаточно изменить в листинге 8.15 последнюю строку, выражающую решение СЛАУ (8.4), на код, реализующий минимизацию численным методом, как это показано в листинге 8.16. Расчеты (которые требуют значительно большего компьютерного времени) дают тот же самый результат, что был приведен на рис. 8.11 и 8.12.
Примечание 3
Попробуйте в расчетах листингов 8.15 и 8.16 взять иную, например, более реалистичную, априорную оценку решения (вместо использованного в них нулевого вектора х0) и посмотреть, как это повлияет на результат.
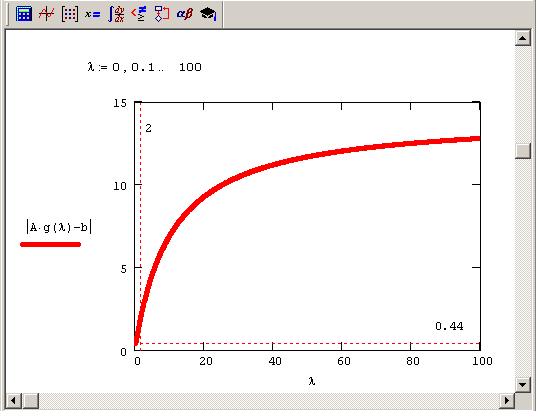
Рис. 8.11. Зависимость невязки регупяризованного решения вырожденной СЛАУ от параметра А. (продолжение листинга 8.15)
Примечание 4
Любопытно также применить вместо формулы (8.3) в качестве функционала Тихонова другую зависимость: Ω(х, λ) = |Ах-b|+ λ |х-х0 |.
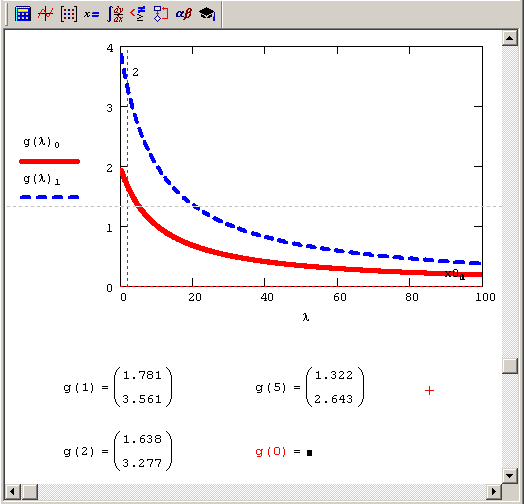
Рис. 8.12. Регуляризованное решение в зависимости от λ (продолжение листинга 8.15)
Листинг 8.16. Регуляризация СЛАУ при помощи алгоритма минимизации (продолжение листинга 8.15):
