QR-разложение
Листинг 8.23. Поиск одного из псевдорешений вырожденной СЛАУ посредством QR-разложения (продолжение листинга 8.22):
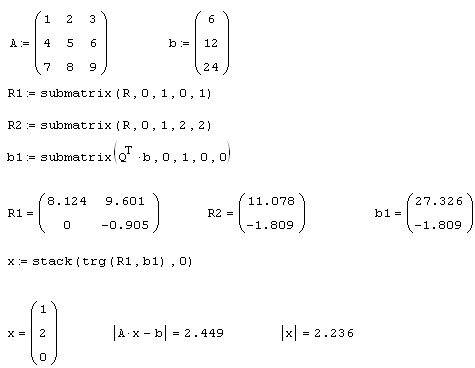
Для того чтобы выбрать из всего множества псевдорешений (минимизирующих невязку исходной СЛАУ) нормальное псевдорешение (т. е. обладающее минимальной нормой), необходимо решить соответствующую задачу минимизации (см. разд. 8.2.3). Если построено QR-разложение, сделать это намного легче. Если произвольную компоненту решения обозначить переменной у: х2=у, то она определится из соответствующей задачи оптимизации (листинг 8.24, 1-3 строки), а остальные составляющие самого решения х – из треугольной СЛАУ R1x=QT b-R2y. В последней строке листинга выводится полученное нормальное псевдорешение, а также его норма и соответствующая норма невязки (которые полезно сравнить с результатом прошлого листинга). Вспомогательный рис. 8.13 помогает понять структуру минимизируемой функции из листинга 8.24.
Листинг 8.24. Нормальное псевдорешение вырожденной СЛАУ (продолжение листингов 8.22 и 8.23):

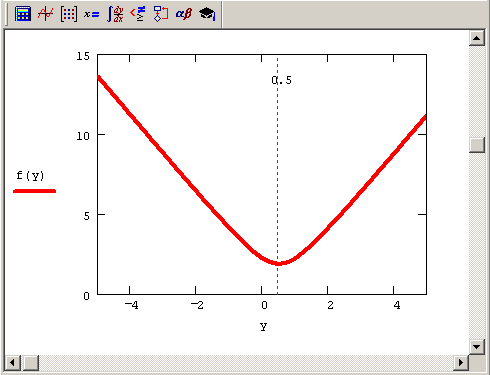
Рис. 8.13. Норма псевдорешения в зависимости от у (продолжение листинга 8.24)
Резюмируя практические аспекты применения QR-разложения, надо отметить, что алгоритмы решения СЛАУ на его основе практически одинаковы как для хорошо обусловленных, так и для сингулярных систем.
Примечание
На прилагаемом к книге компакт-диске вы найдете дополнительные примеры построения QR-разложения как для квадратной, так и прямоугольной матрицы А.
