Графики функций, заданных в параметрической форме
Построение графиков в полярной системе координат возможно двумя способами. Первый способ основан на использовании обычной декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде: x = f x (t) и у= f y (t), где независимая переменная t меняется от минимального значения £ min до максимального t mах с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и т. д. Например, окружность радиусом R может быть задана в следующей параметрической форме: х = R cos(t) и у = R sin(t), если t меняется от 0 до 2п. В общем случае радиус также может быть функцией параметра t.
Для построения параметрически заданных функций используются следующие графические средства:
- ParametricPlot [ {fx, fy}, {t, tmin, tmax} ] – строит параметрический график с координатами f х и f у (соответствующими х и у), получаемыми как функции от t;
- ParametricPlot [{{fx, fy}, {gx, gy},…}, {t, tmin, tmax}] – строит графики нескольких параметрических кривых.
Функции f x, f у и т. д. могут быть как непосредственно вписаны в список параметров, так и определены как функции пользователя.
Рисунок 8.12 показывает построение параметрически заданной фигуры Лиссажу. Она задается функциями синуса и косинуса с постоянным параметром R и аргументами, кратными t. Эти фигуры наблюдаются на экране электронного осциллографа, когда на его входы X и Y подаются синусоидальные сигналы с кратными частотами.
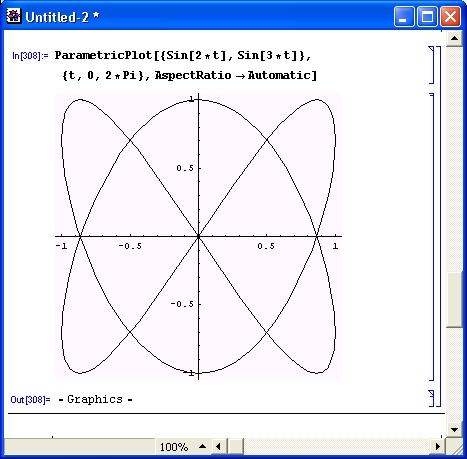
Рис. 8.12. Построение фигуры Лиссажу
