Специальные средства визуализации и звука. Параметрическая трехмерная графика.
Системы Mathematica содержат множество средств, повышающих наглядность представления (визуализации) результатов вычислений – как простых, так и сложных. К ним можно отнести особые виды трехмерной графики, используемые при параметрическом задании поверхностей, в том числе пересекающихся в пространстве, а также графики объемных фигур – полиэдров. Возможности визуализации расширяются при использовании импортируемых рисунков и вставки графических объектов. К специфическим приемам визуализации относится и применение звуковых объектов, способных генерировать и воспроизводить звуки при наличии в компьютере звуковой карты.
Особый шик построениям трехмерных фигур и поверхностей придает функция ParametricPlot3D, в которой предусмотрено параметрическое задание всех трех функций, описывающих координаты точек. Каждая из функций, задающих координаты точек, является функцией двух переменных.
Функция ParametricPlot3D используется в следующих видах:
- PararnetricPlot3D[ {fx, fy, fz}, {t, tmin, tmax}, {u, umin, umax} ] – строит трехмерную поверхность, параметризованную по t и u;
- ParametricPlot3D[{fx, fy, fz}, {t, tmin, tmax}] – создает трехмерную пространственную кривую, параметризованную переменной t, которая изменяется от tmin до tmax;
- ParametricPlot3D[ { fx, fy, fz, s},…] – выполняет затенение графика в соответствии с цветовой спецификацией s;
- ParametricPlot3D[ { {fx,fy, fz}, {gx, gy, gz},…},…] – строит несколько объектов вместе.
Эта функция имеет множество опций, которые можно вывести с помощью команды Options [ParametricPlotSD]. Большая часть из них уже рассматривалась ранее. При этом даже при использовании только опций, заданных по умолчанию, можно получить любопытные построения. На рис. 8.29 показан простой пример применения функции ParametricPlot3D для построения замкнутой линии, расположенной в пространстве. Это, так сказать, объемный вариант, фигур Лиссажу, построение которых было описано ранее.
Параметрическое задание функций позволяет легко строить сложные пространственные фигуры, визуально весьма напоминающие реальные объекты. Покажем это на трех характерных примерах.
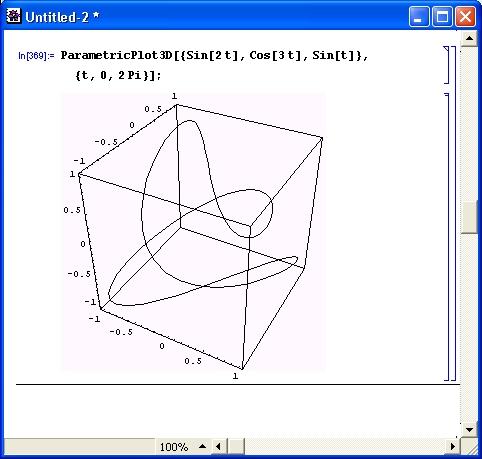
Рис. 8.29. Построение пространственной кривой, заданной в параметрической форме
Первым примером может служить фигура "рог изобилия", показанная на рис. 8.30. По существу, это раскручивающаяся объемная спираль, диаметр которой постепенно нарастает.
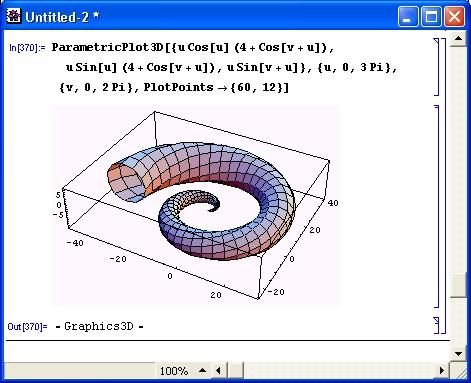
Рис. 8.30. Построение фигуры "рог"
