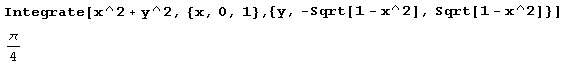Интегрирование
Неопределенные интегралы, или первообразные
Интегрирование в системе Mathematica (как и в жизни) сложнее дифференцирования. Впрочем, формально все просто: неопределенный интеграл вычисляют посредством команды Integrate:
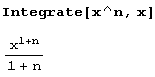
Заметьте, что здесь не учтен случай n = -1. Конечно же, неберущиеся интегралы не берутся.

А вот более сложный пример.

Для человека это уже не совсем просто. Впрочем, в ранних версиях система Mathematica взять этот интеграл не могла.
Определенные интегралы
Команда Integrate умеет вычислять и определенные интегралы, а для тех, которые с ее помощью не берутся, имеется команда NIntegrate, позволяющая вычислять определенные интегралы приближенно. Рассмотрим пример.
Integrate[3x ^ 2, {x, 0, 1}] 1В необходимых случаях выполняются проверки.

Как видите, система Mathematica рассмотрела даже случаи комплексного n. Но есть ведь неберущиеся интегралы… Система не отступает даже перед ними.
Integrate[Sin[Sin[x]], {x, 0, Pi}] π StruveH[0.1]В данном случае система Mathematica выразила значение интеграла через константу и значение специальной функции. Но можно, конечно, вычислить и приближенное значение интеграла.
NIntegrate[Sin[Sin[x]], {x, 0, Pi}] 1.78649Повторные интегралы
Конечно, система Mathematica может вычислять и повторные интегралы.