Матрицы
В системе Mathematica матрицы представляются в виде списков строк, т.е. в виде списков списков. Вот пример задания матрицы. Матрица задается как список списков.
m1={{1.1,1.1},{a,b,c,d},{a^2,b^2,c^2,d^2}} {{1.1,1.1}, {a,b,c,d}, {a2,b2,c2,d2}}Конечно, привычнее ее видеть как матрицу.

Действия с матрицами и векторами задаются естественным образом. Умножим, например, матрицу на вектор.
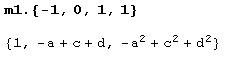
А вот как можно умножить матрицу m1 на скаляр t.

Для квадратной матрицы Mathematica позволяет найти определитель, а также обратную матрицу (если, конечно, матрица обратима, т.е. имеет ненулевой определитель), собственные значения и векторы.
Пусть:
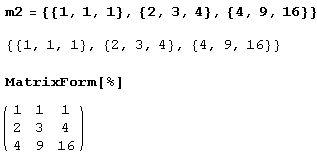
Найдем определитель:
Det[m2] 2Поскольку он ненулевой, можем найти обратную матрицу.
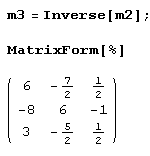
Произведение матрицы на ее обратную должно быть единичной матрицей. Давайте проверим.
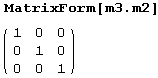
Так и есть!
