Вычисление интегралов
Каверзные интегралы и визуализация результатов интегрирования
Выше мы уже сталкивались с примерами вычисления "каверзных" интегралов. Немного продолжим эту важную тему и заодно рассмотрим приемы визуализации вычислений, облегчающие понимание их сущности.
В Соросовском образовательном журнале (№6, 2000, с. 110) приводятся не совсем удачные примеры вычислений определенного интеграла с применением системы Mathematica, при которых якобы встречаются настолько большие трудности, что они не под силу любому калькулятору или компьютеру. При некоторых попытках вычисления этого интеграла он давал нулевое значение. Но Maple 7 (кстати, как и Mathematica 4) с легкостью берет этот интеграл и позволяет сразу и без какой-либо настройки вычислить для него как точное, так и приближенное значение:
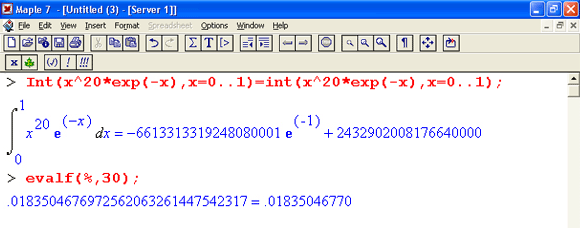
Хотя первое из решений является самым кратким и, скорее всего, единственным точным решением, оно может и должно насторожить опытного пользователя. Дело в том, что в полученном выражении фигурируют большие числа, и потому для правильного приближенного решения (в виде вещественного числа в научной нотации) нужно заведомо использовать аппарат точной арифметики и ни в коем случае не полагаться на погрешность, заданную по умолчанию, – вот в чем основная ошибка в упомянутой статье.
Именно поэтому левая и правая части приближенного решения (выполненного с точностью до 30 цифр) заметно различаются. Знак равенства между ними вызывает чувство протеста у истинных математиков. На самом деле, не надо забывать, что знак равенства здесь был введен просто как текстовый комментарий, – вы можете попробовать сами заменить его на более приемлемый здесь знак приближенного равенства. Любопытно, что предшествующая версия Maple 6 при задании погрешности по умолчанию вычисляла значение этого интеграла также как 0, тогда как Maple 7 "поумнела" уже настолько, что дает значение 0.01835046770 даже в этом случае.
При таких условиях многие читатели могут сомневаться в корректности конечного результата. Между тем Maple 7 позволяет наглядно проиллюстрировать характер промежуточных вычислений подобных интегралов. Например, для этого можно вычислить неопределенный интеграл подобного вида:
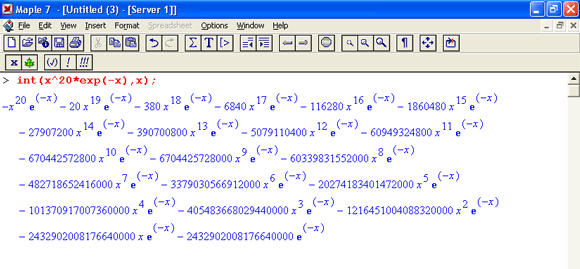
Нетрудно заметить, что решение распадается на множество слагаемых, соответствующих общеизвестному интегрированию по частям. В каждом слагаемом имеются большие числа, и потому принципиально необходимо применение арифметики высокой точности (или разрядности). Maple 7 такими средствами, причем превосходными, обладает.
