Вычисление интегралов
Между тем ситуация вовсе не является безнадежной. Надо просто знать, что предпринять, чтобы подсказать системе правильный путь решения. Например, в нашем случае, применив параметр continuous (в апострофах), можно получить куда более простое выражение:
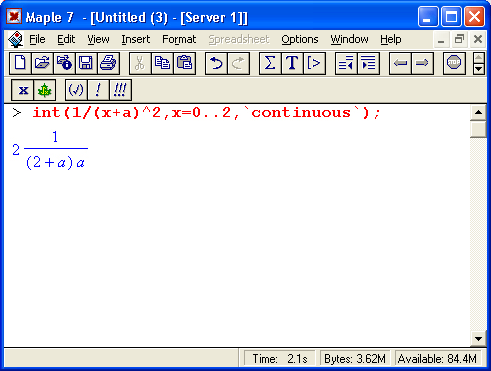
Рисунок 8.3 показывает это решение с двумя важными дополнениями – оно представляется функцией пользователя, а ее график строится при изменении а от -10 до 10.
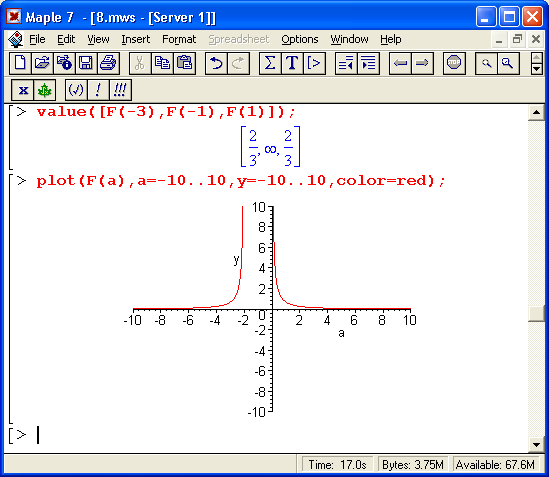
Рис. 8.3. Зависимость значения интеграла с подынтегральной функцией 1/(х+а)^2 и пределами от 0 до 2 от параметра а
Приведем еще один пример "каверзного" интеграла довольно простого вида:
> int(l/x^3,x=-1..2); undefined
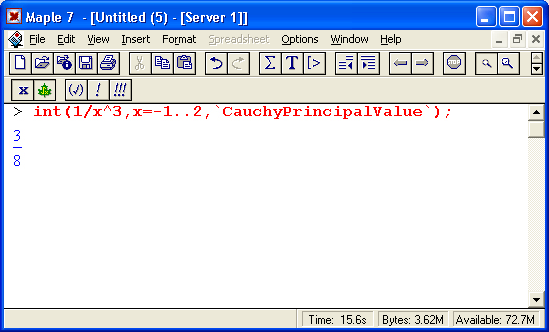
Этот интеграл вообще не берется функцией int без указания параметров (в строке вывода сообщается об этом). Но введение параметра CauchyPrincipalValue позволяет получить значение интеграла: