Вычисление интегралов
Обратите внимание на то, что здесь прямое вычисление интеграла к успеху не привело, хотя из графика функции видно, что каждая положительная полуволна в близкой к t = 0 области явно больше по амплитуде, чем последующая отрицательная полуволна. Однако в отличие от предыдущей функции при больших значениях аргумента данная функция вырождается в обычную синусоиду с неизменной (и равной 1) амплитудой. Вот почему трудяга Maple 7 честно отказывается вычислять интеграл от такой коварной функции.
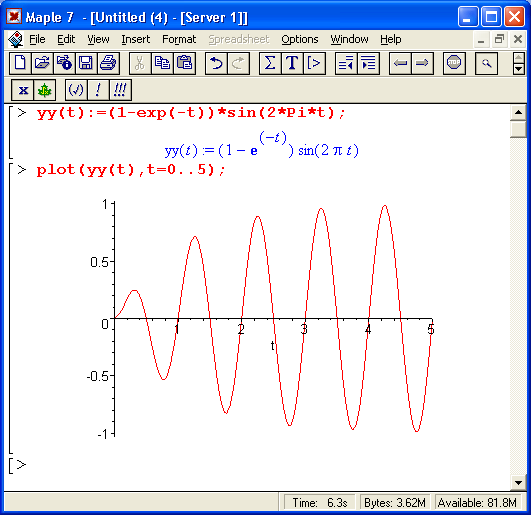
Рис. 8.5. График "экспоненциально нарастающей синусоиды" и интеграл от нее с пределами от 0 до бесконечности
На этом примере очень четко отслеживается разница в мышлении инженера и математика. Инженер скажет, что интеграл с такой функций должен быть, поскольку вначале положительные площади явно меньше отрицательных, а в дальней области они выравниваются, и потому площадь каждого "периода" функции становится примерно нулевой. По-своему инженер прав – если его не интересует точное определение подынтегральной области в заоблачных высотах бесконечности, то мы должны получить то же значение интеграла, что в предшествующем примере, но со знаком "минус". И в самом деле (см. рис. 8.5), интегрируя в пределах от 0 до100π, мы получаем именно это значение (опять-таки в пределах погрешности по умолчанию).
И все же прав здесь математик – переход от интегрирования с конечным (да еще и кратным 2π) пределом к интегрированию с бесконечным пределом – далеко не простая операция. Она требует учета поведения функции при значении аргумента, стремящегося к бесконечности, а тут говорить о нулевой алгебраической площади синусоиды некорректно, ибо никакой кратности величине 2π у бесконечности нет! Остается лишь радоваться тому, что система Maple 7 может примирить математиков и инженеров, дав им в руки средства, позволяющие решать подобные задачи с приближениями, приемлемыми для тех или иных категорий пользователей.
Мы подробно рассмотрели этот класс задач потому, что многие важные интегральные преобразования (например, преобразование Фурье) оперируют с подобными подынтегральными функциями и надо тщательно разбираться в областях их применения.
Примечание
Приведенные выше примеры показывают, что интегрирование является гораздо более тонким делом, чем это кажется на первый взгляд. Тут уместно напомнить, что и студент вуза, и профессор математики университета должны очень внимательно исследовать возможности вычисления интегралов того или иного типа разными математическими системами. Иными словами, применять системы компьютерной математики должны только пользователи, обладающие не столько учеными званиями и степенями, сколько культурой выполнения математических вычислений.
